Probing chiral recognition in liquid chromatography by absolute configuration modulation ATR-IR spectroscopy

Ronny Wirz,^a Davide Ferri,^a* Thomas Bürgi^b and Alfons Baiker^a

^aInstitute for Chemical and Bioengineering, ETH Zurich, Wolfgang-Pauli-Strasse 10, HCI, CH–8093 Zurich, Switzerland. E-mail: [email protected]
^bInstitute of Microtechnology, University of Neuchâtel, Rue Emile-Argand 11, CH–2009 Neuchâtel, Switzerland

Introduction

Separation of enantiomers is of utmost importance in drug research, because of the requirement for high purity grade ingredients for pharmaceutical formulations. Among the various techniques for enantioseparation, chromatographic techniques, such as high-performance liquid chromatography (HPLC), play an important role. Enantiomers interact differently and selectively with a chiral stationary phase (CSP), therefore exhibiting distinct retention times (Figure 1). Stationary phases often consist of porous silica particles modified by complex binding groups (selectors), which are responsible for the selective interaction with the analytes (selectands), thus providing separation. The selectands are injected in the column and eluted with the mobile phase (solvent), which has opposite polarity to that of the CSP. In modern instruments, the separated analytes are identified typically using a UV detector, the main reason being the excellent detection limit of the method. Infrared spectroscopy is also a potent liquid chromatographic detection method¹ and a number of pertinent techniques have been developed in the last two decades.² The advantage of infrared spectroscopy over UV methods is that a direct molecular identification of the analyte can be achieved, given the fact that the IR spectrum of an organic compound provides a unique fingerprint, which makes it distinguishable from other compounds.

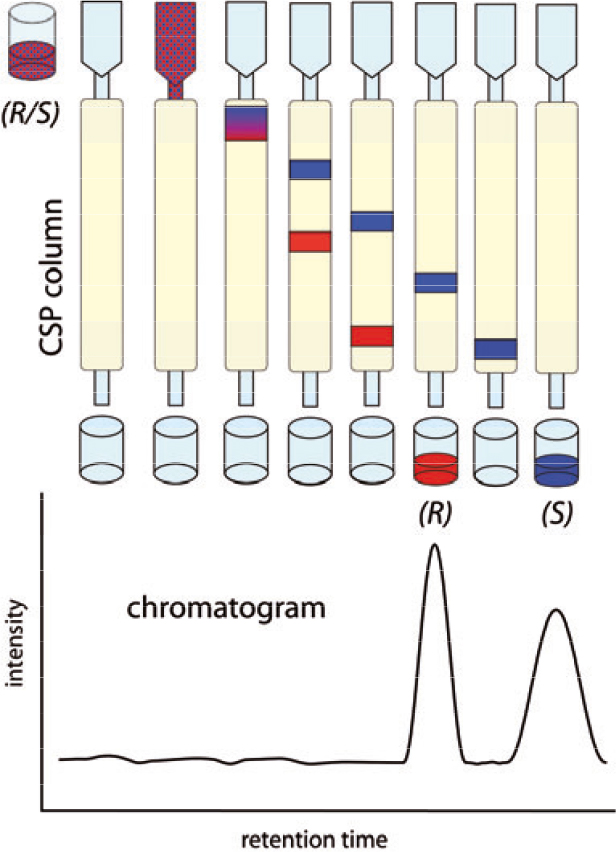
Figure 1. In chiral liquid chromatography a racemic mixture is separated because of the different adsorption strength of the enantiomers on the chiral stationary phase. The less strongly bound enantiomer is eluted faster and shows a shorter retention time.

It is obvious that the interactions occurring at the solid–liquid interface between the CSP and the selectands dissolved in the mobile phase are the essence of an HPLC experiment. The separation of a racemic mixture is based on the different energies of the two diastereomeric complexes that are formed upon interaction between the CSP and the enantiomers. The larger the difference in the free energy between the two diastereomeric analyte–CSP complexes is, the higher is the separation capacity. To successfully separate enantiomers, at least three interactions (three-point model) have to be generated between one enantiomer and the CSP, including attractive (ionic, hydrogen bonding, π–π interaction, van der Waals) and repulsive (steric hindrance) interactions.

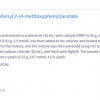
The rational design of a new CSP requires the understanding of the nature of its interaction with the analytes. At this point in situ techniques come into play. The determination of crucial interactions manifesting at solids in contact with liquids is the goal of our research and we pursue this goal applying infrared spectroscopy of the solid–liquid interface, during, for example, the chromatographic event. Hence, we report here on an analytical technique based on the combination of attenuated total reflection infrared (ATR-IR) spectroscopy³ and modulation excitation (ME),⁴ which enables the investigation of the interactions leading to separation at the selectand–selector interface. The potential of the technique is validated for the well-known system given by the enantiomers of N-3,5-dinitrobenzoyl-leucine [DNB-(R,S)-Leu] and tert-butylcarbamoyl quinine (tBuCQN)⁵ immobilised on porous silica particles [Figure 2(c)].

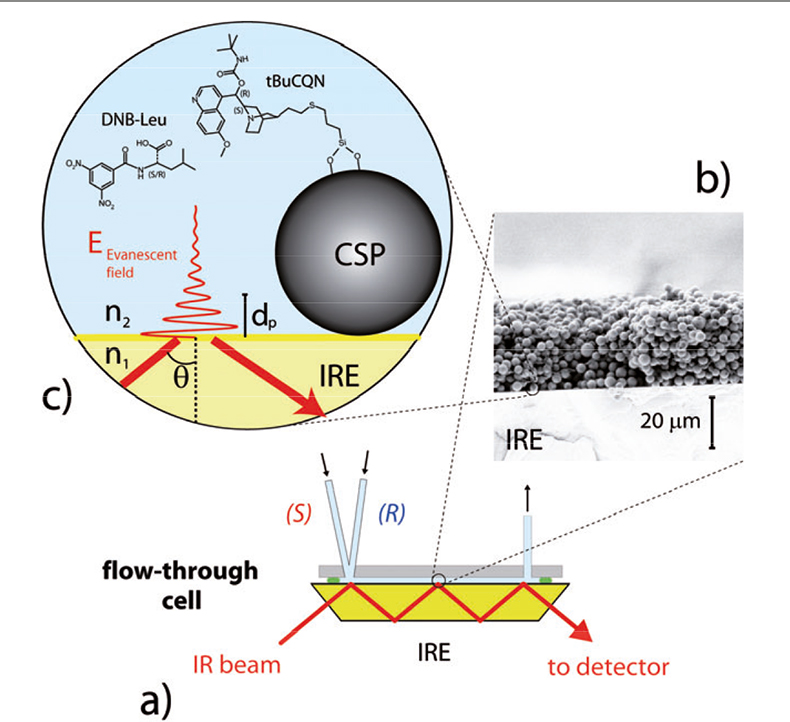
Figure 2. ATR-IR spectroscopy of chiral solid–liquid interfaces. (a) The trapezoidal IRE is mounted in a flow-through cell, where solutions can be periodically admitted. (b) The CSP particles are deposited on the IRE and contacted with each enantiomer dissolved in the mobile phase. (c) An evanescent electromagnetic field is generated into the optical rare medium (n₁ > n₂). Interaction of the vibrational dipoles of the species residing within the CSP layer (the liquid phase, the adsorbed species and the CSP material) and the evanescent field generates IR signals.

Attenuated total reflection infrared (ATR-IR) spectroscopy

The investigation of interactions at solid interfaces using infrared spectroscopy is not trivial when the sample is immersed in a liquid environment, because the bulk liquid (and solid) phase absorbs most of the energy, thus obscuring the typically weak signals originating from species residing at the interface. This problem is overcome in a multiple internal reflection geometry, based on attenuated total reflection Fourier transform infrared (ATR-FTIR or simply ATR-IR) spectroscopy.³ The method is already used for detection in chromatography, the design of proper spectroscopic cells allowing for the remarkable increase of the detection limit to the part per billion region.

In ATR-IR spectroscopy the infrared beam is coupled into an internal reflection element (IRE) [Figure 2(a)]. The latter consists of a material of high refractive index (n₁) and is transparent in the mid-IR, like zinc selenide (or germanium). The geometry of the IRE allows the radiation to be totally reflected once or, in the case of multiple internal reflection, several times before it leaves the IRE. Total internal reflection of an electromagnetic wave occurs at the interface of the IRE and an optically rare medium (the sample, n₂ < n₁) when the angle of incidence of the radiation exceeds the critical angle (θ_c), defined by the law of refraction [sin(θ_c) = n₂/n₁]. At the point of reflection an evanescent electromagnetic field is generated into the sample [Figure 2(c)]. The amplitude of the evanescent field decreases exponentially from the surface of the IRE into the sample. An indication on the fraction of sample probed by the electromagnetic field is given by the penetration depth (d_p),

\[{d_p} = \frac{\lambda }{{2\pi {n_1}\sqrt {{{\sin }^2}\left[ {\theta - {{\left( {\frac{{{n_2}}}{{{n_1}}}} \right)}^2}} \right]} }}\]

(1)

which is the distance from the IRE surface where the electric field vector E drops to a value 1/e of its amplitude at the interface. The penetration depth depends on the wavelength λ, the angle of incidence (θ) and the refractive indices of the IRE and the sample (n₁ and n₂). Typical values of d_p are in the range of 0.1–1.3 μm.

Upon internal reflection no energy is lost if no absorption occurs in the sample. When absorption occurs at the interface, the evanescent field is attenuated and the infrared spectrum of the sample (the analyte) is generated. Now consider a thin film of CSP particles deposited on the surface of the IRE [Figure 2(b)] in contact with a flowing solution. Since only a small volume is probed near the IRE’s surface, what is sampled by the infrared radiation is mainly originating from species residing within the CSP layer, which discriminates signals from the bulk liquid. Therefore, the resulting ATR-IR spectrum consists mainly of information on adsorbate–adsorbate, adsorbate–surface and adsorbate–solute interactions. The ATR-IR method becomes in this way a potential sensor for the crucial interactions involved in enantio separation but requires combination with an additional analytical method to be sensitive enough to differentiate between diastereomeric complexes. This technique is modulation excitation ATR-IR spectroscopy⁴ in which the absolute configuration of the analyte is changed periodically.⁶

Absolute configuration modulation (ACM) spectroscopy

Modulation excitation can be applied for the investigation of reversible systems, the reversibility of the process being an essential requirement. The method is based on the stimulation of the system under investigation by a periodic alteration of an external parameter, e.g. temperature, pressure, electric field, concentration or absolute configuration, in this instance the latter being the designated parameter to investigate chromatographic systems in combination with ATR-IR spectroscopy.⁶ The system will then respond periodically at the frequency of the stimulation. The initial periods of perturbation are needed for the system to reach a quasi-steady state, around which it will oscillate. Therefore, data sampling is started only after the system has reached this equilibrium.

From an experimental point of view, concentration modulation measurements are performed by alternately admitting one enantiomer and the solvent (210 mM acetic acid in acetonitrile in the present case) to the CSP layer using a peristaltic or a HPLC pump. Absolute concentration modulation (ACM) experiments are on the other hand carried out by alternately admitting each enantiomer to the CSP layer; the two diastereomeric enantiomer/CSP complexes are therefore formed and detected alternately on the surface of the particles. The IRE (ZnSe) is coated with a layer of the CSP particles and is mounted in a homemade flow-through cell (total volume, ca 80 μL)⁷ schematically depicted in Figure 2(a).

The resulting data set of a modulation excitation experiment is composed of a series of time-resolved spectra within the modulation period. Since the chemical process under investigation and therefore the system response is reversible many periods can be accumulated and averaged, resulting in spectra with very high signal-to-noise ratio.

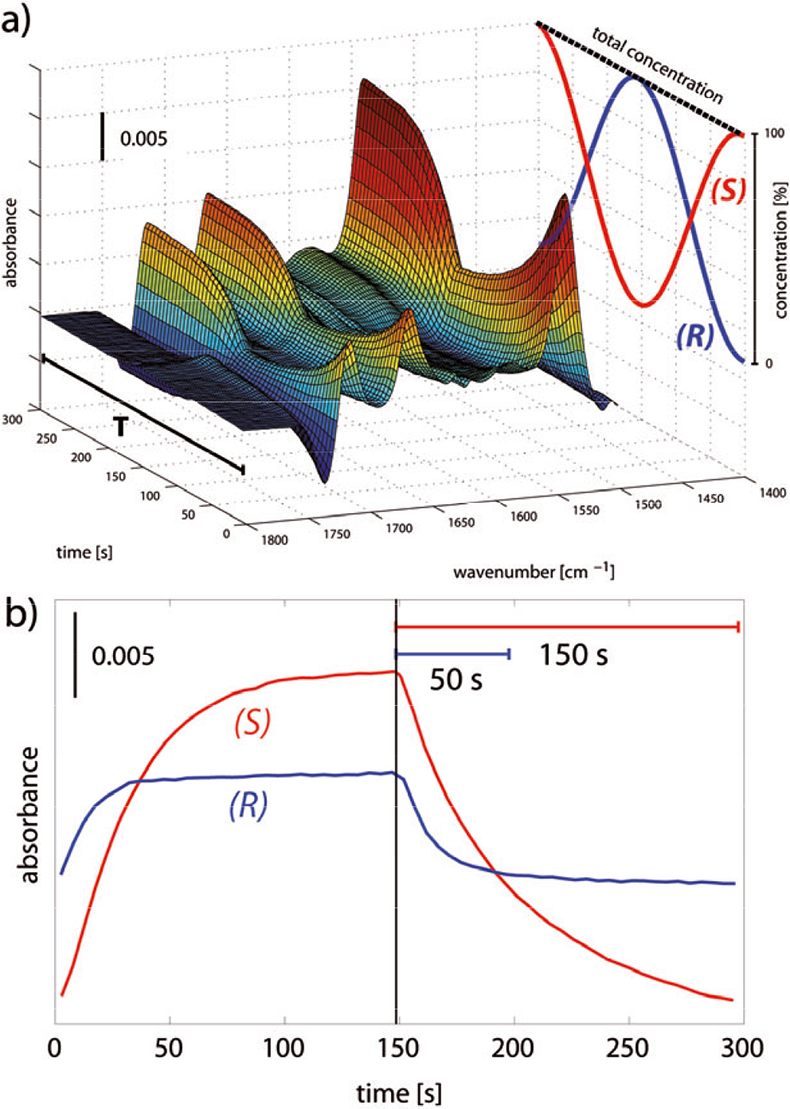
Figure 3. (a) Spectral data in the amide I/II region obtained in an ACM experiment. The CSP was alternately contacted with solutions containing equal concentrations (1 mM) of the (R)- and the (S)-enantiomer of DNB-Leu, resulting in a constant and maximum total concentration within one modulation period T (299 s). (b) Time-dependent response of the signal at 1346 cm^–1 [ν_s(NO₂)] of the two enantiomers of DNB-Leu in two distinct concentration modulation experiments (DNB-Leu 1 mM vs solvent) showing the longer time required to desorb DNB-(S)-Leu. The spectrum where the CSP was contacted with the solvent only served as the reference.

A typical data set collected during an experiment where the absolute configuration is modulated is depicted in Figure 3(a) together with the concentration profiles of the (R)- and the (S)-enantiomer. In contrast to concentration modulation experiments [Figure 3(b)],⁴ the total concentration of both enantiomers does not change within a modulation period T and remains constant throughout the experiment. Signals contributing to the time-resolved spectra originate from dissolved species and from species interacting with the CSP, forming non-specific interactions and/or diastereomeric complexes. It is important to be reminded here that enantiomers exhibit identical infrared spectra; therefore, the corresponding signals remain constant within a modulation period. On the contrary, selective interactions between each enantiomer and the CSP give rise to two diastereomeric complexes that have distinct contributions in their IR spectra. Signals originating from such specific interactions should exhibit a similar periodic behaviour as the stimulation. This is clearly seen in Figure 3(a) where response signals in the 1800–1400 cm^–1 spectral range are shown. Signals of amide I and amide II vibrations, which are very sensitive to hydrogen bond formation, appear typically in this region of the spectrum for the selected chromatographic system. Figure 3(a) shows that most of the signals exhibit the same periodic behaviour as the concentration profile of the (S)-enantiomer. Therefore, it is likely that they originate predominantly from vibrations belonging to the (S)-enantiomer/ CSP complex.⁸ Accordingly, Figure 3(b) shows that in the concentration modulation experiments the time-resolved signal at 1346 cm^–1 [ν_s(NO₂) of DNB-Leu] exhibits different kinetic behaviour for the two enantiomers: DNB-(S)-Leu is more slowly desorbed from the CSP.

An important step in a modulation experiment is the additional elaboration of the time-resolved data set obtained, for example, in Figure 3 using a phase-sensitive analysis (PSA) to obtain phase-resolved spectra according to

\[A_k^{\phi _k^{{\rm{PSD}}}}\left( {\tilde \nu } \right) = \frac{2}{T}\int_0^T {A(\tilde \nu ,t)\sin (k\omega t + \phi _k^{{\rm{PSD}}}){\rm{d}}t} \]

(2)

where k determines the demodulation frequency (k = 1 being the fundamental frequency, and k = 2, 3, ... the first harmonic, second harmonic etc.), T is the duration of the modulation period, φ^PSD is the demodulation phase constant, ω (= 2π/T) is the modulation frequency, and A(\({\tilde \nu }\),t) is the time-dependent absorbance at wavenumber \({\tilde \nu }\) (response signals as depicted in Figure 3). The argument of the sine function is called the phase angle of the demodulation function.

The principle of PSA is depicted in Figure 4, which illustrates the relation between a time-resolved signal at wavenumber \({\tilde \nu }\)₀, characterised by the absorbance A(\({\tilde \nu }\) ,t) and the corresponding phase-resolved signal. The transient signal depicted in Figure 4(a) (red) and the demodulation sine function chosen by the operator (dashed) have the same phase angle and are in phase; and after multiplication they generate a function as depicted in Figure 4(b). Integration over the whole period (green area) and normalisation according to Equation (2) produces the signal at \({\tilde \nu }\)₀ in the demodulated spectra [Figure 4(c)]. The intensity at \({\tilde \nu }\)₀ corresponds to the amplitude of the time-dependent sinusoidal signal. Equation (2) represents an effective filter of signals at frequencies different from the stimulation frequency. Since this holds also for the noise of a signal, which consists mainly of much higher frequencies than the modulation frequency, an increase of about one order of magnitude of the signal-to-noise ratio can be obtained additionally to the improved signal-to-noise ratio gained by co-adding the spectra of several periods.⁶

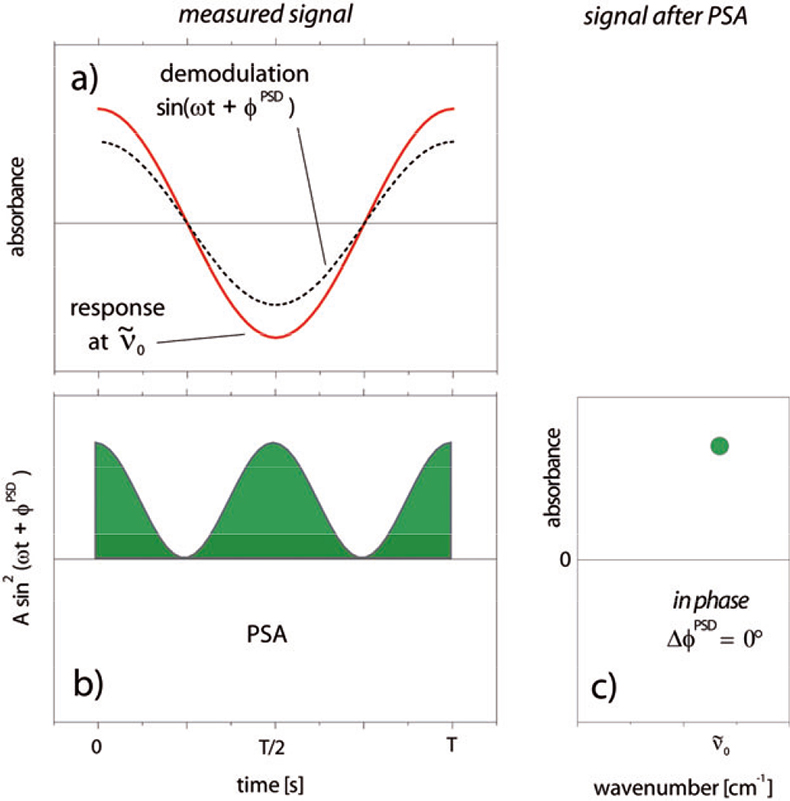
Figure 4. Principle of ACM and PSA. The time-dependent response signal at each wavenumber (\({\tilde \nu }\) ) can be analysed according to Equation (2). A sine function [(a), dashed] with the same phase angle (same frequency ω + same phase constant φ^PSD) as the response signal [(a),red] is multiplied with the response signal leading to a result as depicted in (b). Integration and normalisation of the product over the whole period T gives the in phase spectrum at \({\tilde \nu }\) (c).

The signals of species that are not affected by the stimulation (for example signals of dissolved enantiomers) remain constant within a modulation period and are silent in the phase-resolved spectrum (integrating a sine function over one period equals zero!). This procedure allows for the separation of the static response from the information of interest, or in chromatographic terms the separation of dissolved and non-specifically bound species from the enantio-specifically interacting enantiomer/CSP complex.

Figure 5(a) shows the in phase spectrum resulting from the PSA of the time-resolved data set shown in Figure 3.⁸ For the reasons mentioned above, every signal observed in the phase-resolved spectrum of the ACM experiment [Figure 5(a)] originates only from the interface where the enantiomers form diastereomeric complexes with the CSP. No signal from dissolved species of DNB-Leu is observed, e.g. the signal at ca 1750 cm^–1 [ν(COOH), Figure 5(d)]. For comparison with the ACM experiment, in phase spectra of concentration modulation experiments are reported where the (S)-enantiomer (red) and the (R)-enantiomer (blue) were modulated against the neat solvent, i.e. the net concentration changed from 0 % to 100 % within the modulation period. In fact, spectrum (a) is the difference between the (S)-enantiomer/CSP and the (R)-enantiomer/CSP complexes. In contrast to the ACM experiment, the signals observed in the concentration modulation spectra originate from adsorbate–surface interactions and from dissolved species. It is obvious from Figure 5(a) and (b) that the demodulated spectrum of the ACM experiment contains mainly signals originating from the (S)-enantiomer/CSP complex. Spectra (a) and (b) deviate considerably from the spectrum of the dissolved enantiomer(s) [Figure 5(d)]. Note the appearance of the signals at 1715 cm^–1 and 1585 cm^–1 concomitant with the negative signal at 1735 cm^–1. Comparison with a spectrum of the analogous of tBuCQN in the liquid state indicates that these features rationalise the response of the CSP surface to a specific bonding with the functional groups of the (S)-enantiomer. The positive signal at 1715 cm^–1 originates from the amide group of the CSP hydrogen bonded to the enantiomer. The vibration associated with this group red-shifts upon interaction and gives rise to the negative signal at 1735 cm^–1. On the contrary, the (R)-enantiomer [Figure 5(c)] exhibits much weaker signals on the CSP and a rather similar spectrum to that recorded in the absence of the CSP. Therefore, no specific hydrogen bond occurs between this enantiomer and the CSP, which is further corroborated by the absence of the negative signal at 1735 cm^–1. The observed difference in signal intensities between spectra (a), (b) and (c) reveals also that the concentration of the (S)-enantiomer at the CSP is higher than that of the (R)-enantiomer, thus supporting the order of elution of the two enantiomers.⁵

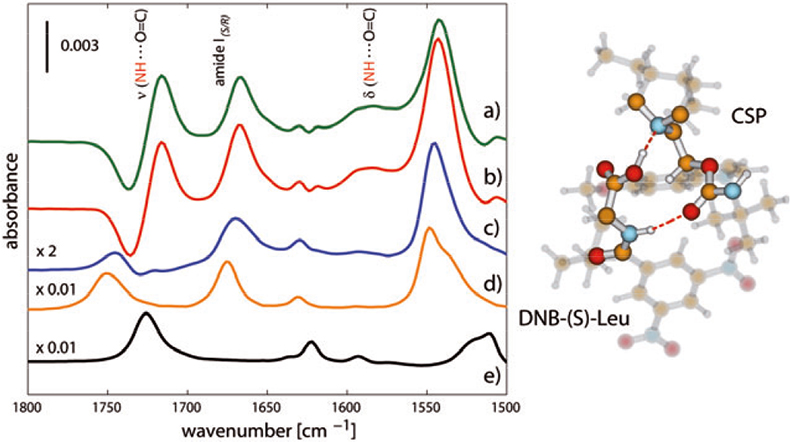
Figure 5. Left panel: demodulated in phase spectra of modulation excitation experiments. (a) ACM experiment [DNB-(S)-Leu vs DNB-(R)-Leu]: the signals originate exclusively from molecular vibrations involved in the diastereomeric interactions between the enantiomers of DNB-Leu and the CSP. (b) and (c) concentration modulation experiments [DNB-(S)- and DNB-(R)-Leu vs solvent, respectively]. (d) Transmission IR spectrum of dissolved DNB-(S)-Leu, 50 mM [the DNB-(R)-Leu spectrum would be identical]. (e) Transmission IR spectrum of dissolved tBuCQN (50 mM). Right panel: artist’s view of the structure of the diastereomeric complex generated by interaction of the most strongly bound DNB-(S)-Leu with the CSP that rationalises the spectrum (a).

It can be concluded from the assignment of the observed signals⁸ that the driving force for the stronger binding of the (S)-enantiomer and therefore for the separation of the two enantiomers is the enantio-specific hydrogen bonding between the amide N–H group of DNB-(S)-Leu and the carbamate C=O group of the CSP.⁸ The right panel of Figure 5 shows a possible molecular structure of the diastereomeric complex that rationalises the spectrum in Figure 5(a). Computational methods serve to assign a proper structure and allow one to interpret the changes observed in the spectra at chiral solid–liquid interfaces.⁸ Additionally to the enantio-specific interaction, both enantiomers exhibit a non-specific acid–base interaction between the tertiary nitrogen atom of the quinine moiety of the tBuCQN and their carboxylic group, and π–π interactions between aromatic rings.⁵ The interpretation of the spectrum depicted in Figure 5(a) allows the identification of the functional groups of the selector and the selectand interacting with each other and provides indications on the structure of diastereomeric complexes on a molecular level. Therefore, the technique presented here closes the gap between “model studies” based on the crystal structure of solids and nuclear magnetic resonance (NMR) of analogues of the components of the chromatographic system.

The enantio-specific interaction demonstrated in Figure 5(a) and the obvious different appearance of the spectra in Figure 5(b) and (c) indicate that the interaction between the CSP and DNB-(S)-Leu is strong. This also implies that most of the features observed in the time-resolved spectra [Figure 3(b)] are identical to the features found in the phase-resolved spectra [Figure 5(a)]. Although this is an excellent example to demonstrate the potential of ACM for chromatographic applications, it does not allow one to properly discuss the peculiar advantages of ACM and PSA, e.g. the increase of the signal-to-noise ratio by about one order of magnitude and the separation of dynamic signals originating from enantio-specific interactions from the static signals of dissolved and non-specifically adsorbed species often dominating the spectrum.

Figure 6 shows a chromatographic study more representative for this purpose.⁶ In this case the degree of interaction between the enantiomers of ethyl lactate and the more complex CSP (a polysaccharide derivative)⁹ is very similar and interactions appear weaker compared to the DNB-Leu/tBuCQN system. The time-resolved spectra obtained during a concentration modulation experiment clearly exhibit a poorer signal-to-noise ratio compared to the spectra in Figure 3(b). The in phase spectra in Figure 6(c) and (d) demonstrate the higher signal-to-noise ratio and quality of spectra achieved using the modulation technique.

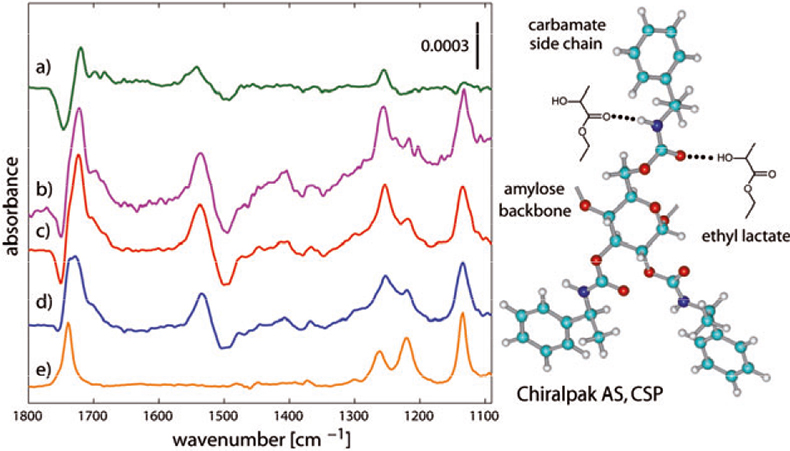
Figure 6. Left panel: demodulated in phase spectra of modulation experiments for the (R)- and (S)-enantiomers of ethyl lactate (EL) on Chiralpak AS. (a) ACM experiment [(R)-EL vs (S)-EL]; (c) and (d) concentration modulation experiments [(R)- and (S)-EL vs solvent, respectively]. (e) Concentration modulation experiment as in (c) and (d) but without CSP [(R)-EL and (S)-EL, identical, 1.8 mM]. (b) Time-resolved spectrum of the concentration modulation experiment corresponding to spectrum (c). Right panel: artist’s view of plausible selectand–selector interactions [the (R)-enantiomer binds to the CSP more strongly].

The ACM spectrum obtained after modulation of the two enantiomers against each other [Figure 6(b)] additionally demonstrates the excellent separation between signals of dissolved species (for example at ca 1740, 1220 and 1140 cm^–1) and signals of species interacting at the CSP surface. Dissolved species clearly appear strong in the concentration modulation experiments since interaction between the enantiomer(s) and the CSP is weak. This better signal resolution is shown in the ACM spectrum illustrating how complex features observed between 1800 cm^–1 and 1650 cm^–1 are better deconvoluted providing only information on species interacting at the surface of the CSP and on the response of the CSP material.

The two examples described clearly demonstrate the value and potential of probing chiral recognition in liquid chromatography by absolute configuration modulation ATR-IR spectroscopy.

Acknowledgements

The authors wish to acknowledge the financial support from the Foundation Claude and Giuliana. We thank Professor U.P. Fringeli and Dr D. Baurecht (University of Vienna) for fruitful discussions on ME spectroscopy and Professor Lindner (University of Vienna) as well as Chiral Technologies-Europe (Illkirch) for providing the cinchona- and amylose-based CSP, respectively.

References

1. G.W. Somsen, T. Visser, ‘‘Liquid chromatography/Infrared spectroscopy’’, in Encyclopedia of Analytical Chemistry, Vol. 12, Ed by R.A. Meyers. John Wiley, Chichester, pp. 10,837–10,859 (2000).
2. J.M. Chalmers and P.R. Griffiths (Eds), Handbook of Vibrational Spectroscopy, Vol. 2. John Wiley, Chichester (2002).
3. N.J. Harrick, Internal Reflection Spectroscopy. Interscience Publishers, New York (1967).
4. D. Baurecht, G. Reiter, N. Hassler, M. Schwarzott and U.P. Fringeli, “Application of special FTIR ATR techniques for quantitative structural analysis of thin surface layers”, Chimia 59, 226–235 (2005). doi: https://doi.org/10.2533/000942905777676524
5. M. Lämmerhofer and W. Lindner, “Quinine and quinidine derivatives as chiral selectors I. Brush type chiral stationary phases for high-performance liquid chromatography based on cinchona carbamates and their application as chiral anion exchangers”, J. Chromatogr. A 741, 33–48 (1996). doi: https://doi.org/10.1016/0021-9673(96)00137-9
6. R. Wirz, T. Bürgi and A. Baiker, “Probing enantiospecific interactions at chiral solid-liquid interfaces by absolute configuration modulation infrared spectroscopy”, Langmuir 19, 785–792 (2003). doi: https://doi.org/10.1021/la026568y
7. Urakawa, R. Wirz, T. Bürgi and A. Baiker, “ATR-IR flow-through cell for concentration modulation excitation spectroscopy: diffusion experiments and simulations”, J. Phys. Chem. B 107, 13,061–13,068 (2003). doi: https://doi.org/10.1021/jp0359889
8. R. Wirz, T. Bürgi, W. Lindner and A. Baiker, “Absolute configuration modulation attenuated total reflection IR spectroscopy: An in situ method for probing chiral recognition in liquid chromatography”, Anal. Chem. 76, 5319–5330 (2004). doi: https://doi.org/10.1021/ac049428x
9. Y. Okamoto and E. Yashima, “Polysaccharide derivatives for chromatographic separation of enantiomers”, Angew. Chem. Int. Ed. 37, 1020–1043 (1998). doi: https://doi.org/10.1002/(SICI)1521-3773(19980504)37:8<1020::AID-ANIE1020>3.0.CO;2-5