Antony N. Daviesa,b and Marcel Simonsa
and Marcel Simonsa
aStrategic Research Group – Measurement and Analytical Science, Akzo Nobel Chemicals b.V., Deventer, the Netherlands
bSERC, Sustainable Environment Research Centre, Faculty of Computing, Engineering and Science, University of South Wales, UK
Many years ago, I was involved in a project where for a short while I dreamt of exploiting the capabilities of nuclear magnetic resonance (NMR) spectroscopy to look at differently bound silicon oxide environments. The complexities of finding an NMR expert who had the capability and the time, and the willingness to convert their instrument for these measurements on nuclei with low abundances and often complex spin systems were enormous. The timeframe of the project meant that I had to give up on what looked a very quick and promising solution to my problem. Ever since that experience, I have generally avoided the ordeal of locking horns with NMR experts and confined myself to the peaceful waters of familiar spin ½ carbon-13 and proton NMR spectroscopy. I am pleased to say that I was recently shaken out of my comfort zone by an NMR expert not only carrying out measurements on these interesting nuclei but also happy to go out and preach about their usefulness. Marcel Simons enthusiastically presented how developments in the available hardware, higher field instruments, better multinuclear probes including cryoprobe options, the spectrometer control systems and also desktop NMR data processing software had all combined to make the measurement of inorganic nuclei a potentially commonplace and very helpful, often complementary, technique to other spectroscopic analytical tools.
Table 1. Some common isotopes useful for NMR analyses and their relative sensitivities assuming equal T1 and T2 relaxation times and temperatures.
Nucleus | Natural abundance (%) | Spin (I) | Magnetic moment µ (µZ/µN) | Gyromagnetic ratio (γ) | Molar sensitivity (rel. 1H) | Receptivity natural ab. (rel. 1H) |
1H | 99.99% | 0.5 | 2.793 | 26.7522 | 1.0000 | 100.000% |
7Li | 92.41% | 1.5 | 3.256 | 10.397704 | 0.2940 | 27.100% |
11B | 80.10% | 1.5 | 2.689 | 8.584707 | 0.1650 | 13.200% |
13C | 1.07% | 0.5 | 0.702 | 6.7283 | 0.0159 | 0.018% |
23Na | 100.00% | 1.5 | 2.218 | 7.0808516 | 0.0927 | 9.270% |
25Mg | 10.00% | 2.5 | –0.855 | –1.63884 | 0.0027 | 0.027% |
27Al | 100.00% | 2.5 | 3.642 | 6.976278 | 0.2070 | 20.700% |
29Si | 4.69% | 0.5 | –0.555 | –5.31903 | 0.0079 | 0.037% |
35Cl | 75.76% | 1.5 | 0.822 | 2.6241991 | 0.0047 | 0.358% |
39K | 93.26% | 1.5 | 0.392 | 1.2500612 | 0.0005 | 0.048% |
79Br | 50.69% | 1.5 | 2.106 | 6.725619 | 0.0795 | 4.030% |
81Br | 49.31% | 1.5 | 2.271 | 7.249779 | 0.0995 | 4.910% |
135Ba | 6.59% | 1.5 | 0.839 | 2.67769 | 0.0050 | 0.033% |
Sensitivity myth and legends
One of the biggest issues in the past has been the lack of sensitivity of NMR instrumentation to the “exotic” nuclei. For those unfamiliar with the technique, it is worth remembering that essentially only isotopes that contain an odd number of protons and/or neutrons have a magnetic moment and angular momentum to be detected by NMR spectroscopy. Other isotopes with even numbers of protons and/or neutrons have zero spin and cannot be detected. The basic sensitivity of any particular nuclei is a function of the relative abundance (natural concentration of the NMR active isotope) and the magnetic moment. Of course, for the analysis of nuclei whose measurable isotopes are only present in very low abundances it is always an option to select experiments which use isotopically enriched samples. However, this is generally an expensive option, not available to many except in very special cases, and not really a solution for day-to-day analysis.
So, if you successfully persuaded your NMR experts to carry out these inorganic experiments it often used to mean tying down the instrument for long periods not only to convert to a different probe head but simply to acquire enough scans in order to deliver a good enough signal-to-noise ratio to allow meaningful interpretation of the data received. The basis for this can be easily seen in Table 1, where the natural abundance, spin state and magnetic moment for a few common NMR inorganic isotopes is given. The term relative receptivity is used as a more useful guide to nuclear response. It is the product of the relative sensitivity and the isotopic natural abundance compared to the proton. So, the myth of insensitivity of the inorganic isotope in NMR over organics can be debunked to a certain extent if we look at the receptivity of 13C, where the relative receptivity compared with 1H is 0.0159 × 1.108 = 0.018%. All the common inorganics selected for Table 1 do better than 13C! Of course, the absolute concentration of carbon in the sample also plays a key role in the final signal-to-noise ratio of the measurement compared to proton NMR spectroscopy. So for scientists concentrating on organic or organometallic chemistry, this is something of a spurious comparison. But it is worth remembering that it is not the sensitivity of the inorganic isotopes themselves in NMR which are inhibiting factors in their own right.
Effect of field strength etc.
Stronger magnets have greatly helped deliver better signal-to-noise ratios. Doubling the field strength, say going from 300 MHz to 600 MHz instruments, whilst keeping everything else constant, doubles the population difference induced in the sample (Boltzmann distribution). Additionally, the current in the probe head doubles whilst only increasing the noise in the head by (overall improvement effect in the probe head = 2 / = 1.4142) giving an overall beneficial increase in signal-to-noise from the doubling of 2 × 1.4142 = 2.8284, everything else being equal.
An additional beneficial effect is the narrowing of the linewidth achieved, as this can bring weak signals out of the noise in some cases. Table 2 summarises some of the factors discussed above and some additional considerations which will influence the applicability of inorganic NMR spectroscopy in the day-to-day operation of your spectroscopic laboratory. Some are influenced by the specific isotope to be analysed, some on the available instrumentation including probe types and bores available, where some effects are down to the molecular environment of the isotope being measured.
Table 2. Some influences on the sensitivity of inorganic NMR of particular isotopes.
Sample/isotope factors |
|
Instrumentation factors |
|
Decoupling and multidimensional experiments, LOQs
As with the more widely used isotopes a range of revealing experiments are also available for the inorganic isotopes. Figures 1 and 2 show the beneficial effect of a proton decoupling experiment on a 119Sn spectrum.
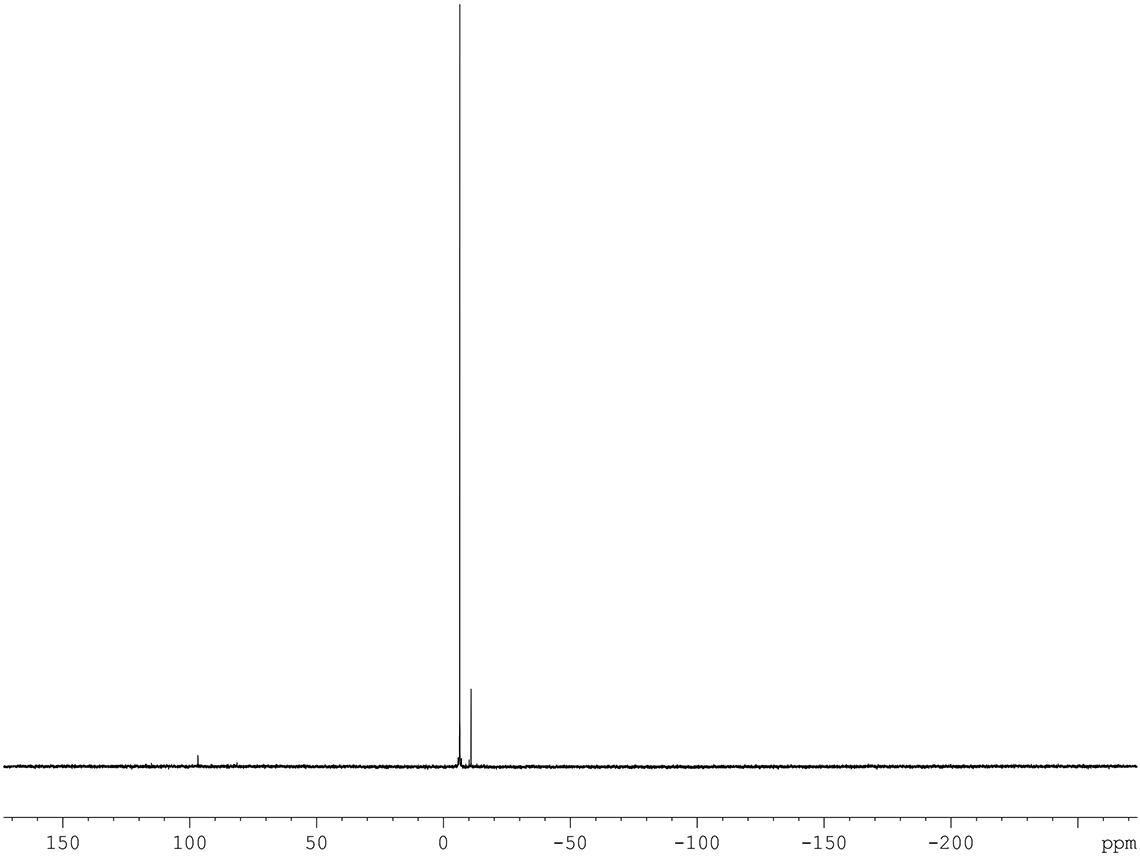
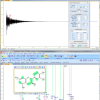
Figure 1. 119Sn spectrum of 145 mg sample in 1.1 g CDCl3 with 0.03% TMS standard.
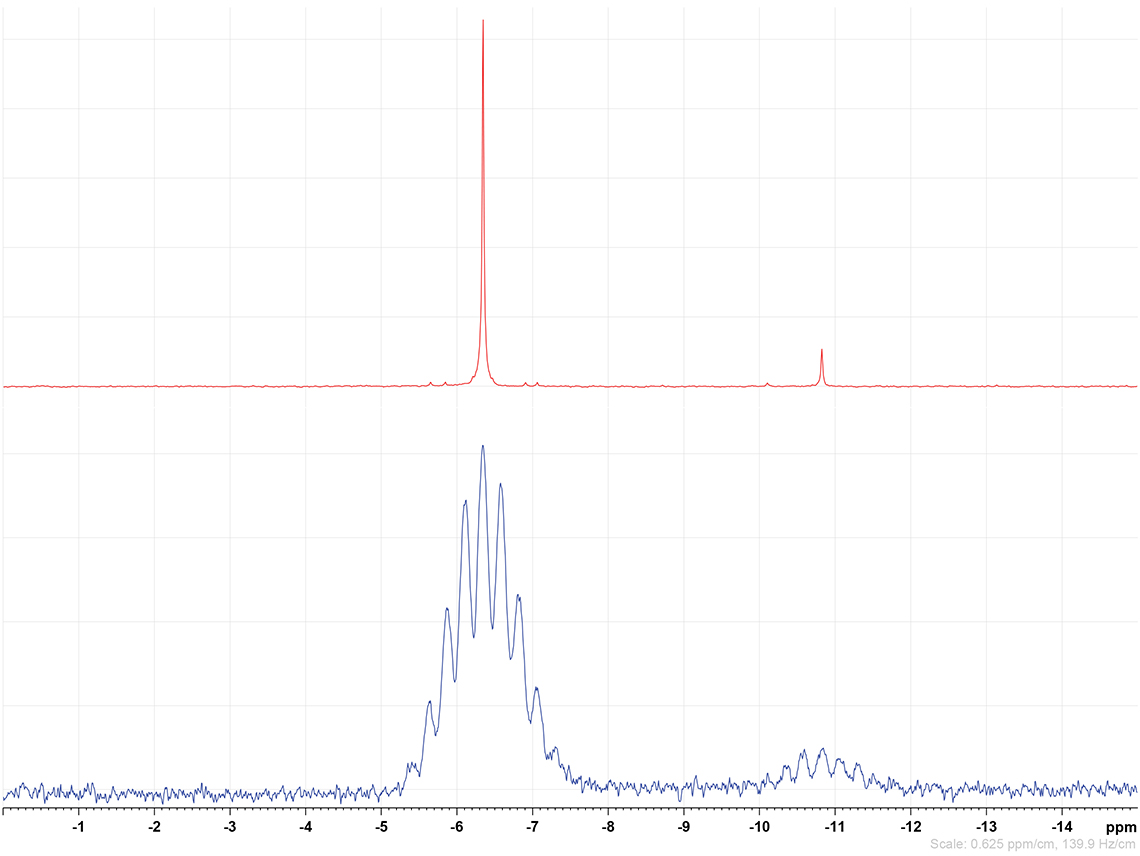
Figure 2. Detail of the same 119Sn spectrum of 145 mg sample in 1.1 g CDCl3 with 0.03% TMS standard showing (bottom) the original coupled measurement and (top) the beneficial effect of a proton decoupling experiment on the signal-to-noise ratio. All in all, for an average 1 h single-dimensional experiment limits of quantification based on 10× signal-to-noise ratio are commonly around achievable in the 10s of mg kg–1 range.
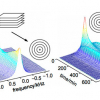
However, multidimensional spectroscopy experiments can also apply to inorganic isotopes, and Figure 3 is an example of a multidimensional NMR experiment which can give great insight into connectivity and arrangement of the inorganic moieties in complex structures. Here the longer-range couplings (2–4 bonds) are revealed in a heteronuclear multiple bond correlation (HMBC) experiment.1–3
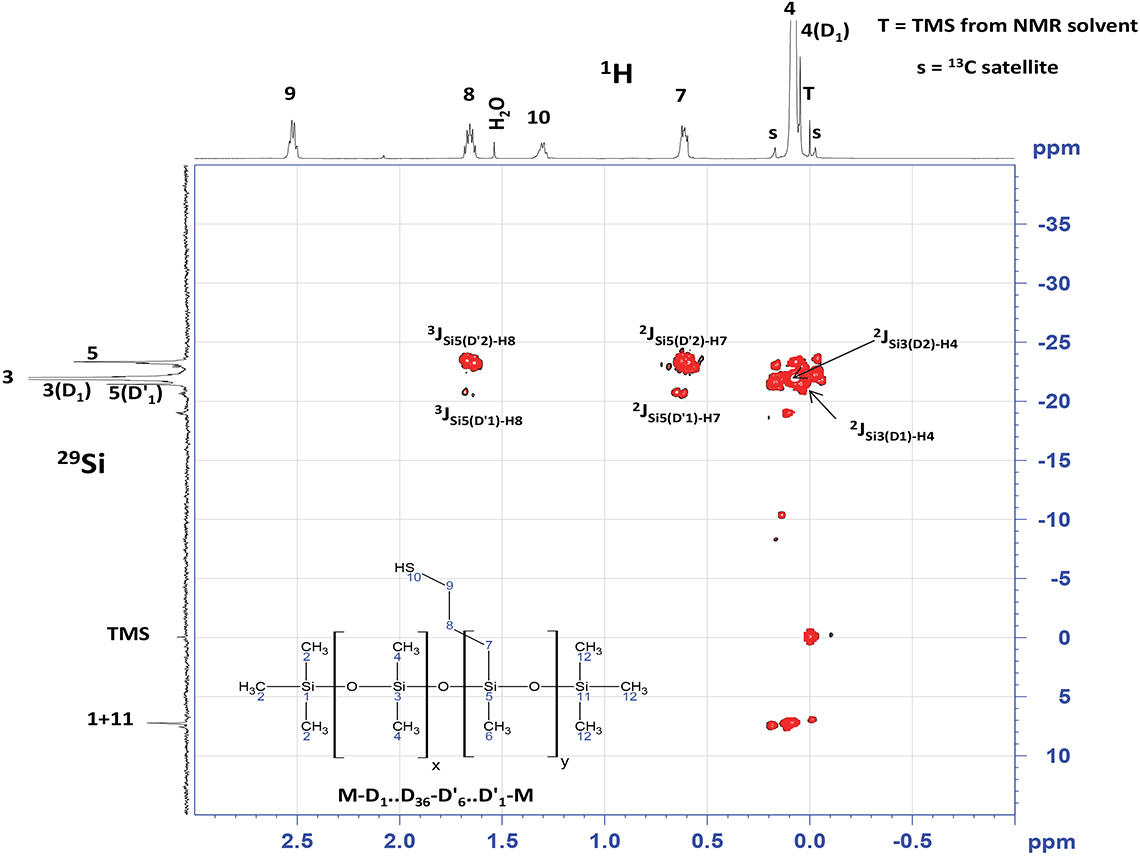
Figure 3. 29Si NMR spectrum 1H,29Si HMBC experiment with peak assignments. 66 mg sample, 1500 mg CDCl3.
Conclusions
I have been surprised how easy it has become to execute inorganic NMR experiments delivering good insights into samples in ways no other technique can deliver. Marcel has convinced me that we can get far more information out of our samples now, with comparatively little effort compared to earlier years and older instrument generations. We can only recommend that you try it out for yourselves—you might be extremely pleased at the outcomes!
References
- A. Bax and M.F. Summers, “Proton and carbon-13 assignments from sensitivity-enhanced detection of heteronuclear multiple-bond connectivity by 2D multiple quantum NMR”, J. Am. Chem. Soc. 108, 2093 (1986). https://doi.org/10.1021/ja00268a061
- E.A. Williams and J.D. Cargioli, “Silicon 29 NMR spectroscopy”, in Annual Reports on NMR Spectroscopy, Vol. 9, Ed by G.A. Webb. Academic Press, p. 221 (1979). ISBN: 978-0125053099
- M. Witanowski, “Nitrogen NMR spectroscopy”, Pure Appl. Chem. 37, 225–233 (1974). https://doi.org/10.1351/pac197437010225