Pentti Minkkinena,b and Kim H. Esbensenc
aPresident, Senior Consultant, SIRPEKA Oy. E-mail: [email protected]
bProfessor emeritus, Lappeenranta University of Technology, Finland
cKHE Consulting (www.kheconsult.com) and Guest professor (Denmark, Norway, Puerto Rico). E-mail: [email protected]
Following the previous column “TOS: pro et contra”, we now present a topic that is exclusively positive and constructive. We have enlisted a looming figure in the TOS panoply, Professor emeritus Pentti Minkkinen, erstwhile of Lappeenranta University of Technology, Finland, to take the lead. A initial survey of possible themes for this column quickly developed into a feast of title alternatives:
- “You will not believe how much it costs not to follow TOS”
- “Following TOS will save you a lot of money (pun intended)”
- “Save now—pay dearly later”
- “It’s not so expensive as you think to follow TOS”
- “The tighter the budget the more important is to use it wisely”
There can be no doubt what is presented below then. “Follow the money” would appear to be a useful lead to follow when matters of “TOS or not, that is the question” come up. Below the reader is presented with salient case histories and examples all focusing on the potential for economic loss or gain—by following, or more importantly, by not following TOS.
Case 1: Always mind your analysis
Incorrect sampling operations can cause huge economic losses to industry. The impact from inferior, insufficient or incorrect sampling and assaying can be tremendous.
On the other hand, when the Sampling Theory is applied correctly, a considerable amount of money can be saved. Would you believe that a difference in average analytical values of only 0.06 % could accrue lost revenue of ~US$300 M in the mining industry? The mind boggles, but read on. The first case study focuses on the analytical part of the full sampling-and-analysis pathway in a copper mine operation:1

A copper mine—this particular mine has no relationship to the case history described in the text.
In 1970 a chemical laboratory of a large copper mining operation in Northern Chile was experiencing a bad response time because of the large amounts of samples to be assayed. The analytical method at the time was atomic absorption. In order to improve the performance, the chief chemist decided to change to XRF. The change reduced the cost and the response time. Only one geological matrix (high-grade secondary sulfides) was considered for calibration. Neither blind duplicates, nor standard reference materials were used at the time in order to monitor the precision and accuracy of the assaying process. This particular mining company was reasonably assured of its general performance because a considerable amount of effort and consulting had been spent to deal with the potentially fatal sampling issues if not heeded with respect to the principles laid down by TOS. In fact this company rightly prided itself of this attitude, which at the time was indeed quite extraordinary. All seemed to go the right way then…
Meanwhile, exploration geologists were also beginning to send samples from a neighbouring deposit to the laboratory for copper assay as well. This matrix was very different, however, copper oxides. Because this fact was not reported to the analytical chemist, the resulting assays, based on the sulfide calibration, turned out to be biased by 0.06 % copper—when a later reckoning was due. This bias may not seem to amount to much, but circumstances were deceiving.
Considering a yearly mining rate of 32 million tons, a recovery of 80 %, an operational lifetime of 20 years, a price of US$1 per pound of copper (contemporary prices) and a discount rate of 10 %, the economic bias caused by the analytical bias could be estimated to be US$292 M.
This was estimated as follows (the following equations are generic and can be used for quite a range of other projects in need of a similar professional economic evaluation):
\[{B_i} = \left[ {{V_i}\left( m \right) - p\left( t \right)} \right] \bullet t_i^{1 - {e^{iN}}} - I\left( t \right)\](1)
where Bi = net present value (M $); Vi(m) = value of one ton of ore ($); p(t) = cost of production of 1 ton of ore at $5 per ton; t = annual rate of production (ton/year) = 30 Mt/year; i = discount rate = 10 %; N = life of mine (years) = 20 years; I(t) = investments (M $) = $640 M; m = mean grade above cut-off grade (%Cu); Vi(m) = 22.4 • pr • R • m; where pr = copper price = 0.8 $/lb, R = metallurgical recovery in % = (m – 0.1008) • 0.9/m. From Equation 1, with a little rearranging:
\[{B_1} = \left[ {{V_1}\left( m \right) - p\left( t \right)} \right] \bullet t_i^{1 - {e^{iN}}} - I\left( t \right)\](2)
\[{B_2} = \left[ {{V_2}\left( m \right) - p\left( t \right)} \right] \bullet t_i^{1 - {e^{iN}}} - I\left( t \right)\](3)
\[\Delta {B_i} = \Delta {V_i}\left( m \right) \bullet t\frac{{1 - {e^{iN}}}}{i}\](4)
\(\Delta V\left( m \right) = 22 \bullet Pr \bullet R \bullet \Delta m\) then the economic bias in net percent values is, when inserted into Equation 4:
\[\Delta {B_i} = 1.056 \bullet 32 \bullet \frac{{1 - {e^{ - 0.1 \bullet 20}}}}{{0.1}} \approx \;\](4)
The lessons from Case Study 1 are:
- The economic consequences of analytical biases can be of considerable magnitude. In the example of a low-grade mineral deposit, the magnitude was similar to the estimated profits.
- Analytical accuracy is essential for correct economic assessment of a mining project—but, of course, the ultimate target for accuracy is the target lot, the full mineralisation. Clearly the ultimate objective is to get a reliable assay in this context, not just a representative sample.
- Communication between corporate protagonists is just as relevant as alignment with the overall business objectives.
- Systematic use of blind duplicates, reference materials (RM) and blanks is crucial in order to assure the quality of the full sampling-and-analytical process. This approach would have discovered the unfortunate consequences demonstrated in this case at a very early date.
Case 2: Saving a client from a fatally wrong, expensive investment
Finely ground limestone is much used as a high-quality coating in the paper industry. But accidental “coarse particles” (i.e. particles larger than 5 µm) in coatings often result in severe defects in high-speed printing machines that may actually break the paper web, which leads to very expensive production stops that must be avoided “at all costs”. There is no room for neglecting this problem in the printing paper industry. The quality of the coating product must comply with the stringent demand of < 5 such particles in every ton of ground limestone coating.
The manager at a limestone coating producer was considering buying an expensive particle size analyser for on-line quality control in order to deal effectively with this issue. The question was would this be an economically viable solution?

Paper manufacture. N.B. The example outlined in the text has no relationship to this particular machine or company.
Let’s ask TOS. Part of the armament of a sampling expert is a thorough knowledge of the features and the use of the classical statistical Poisson distribution. For the uninitiated, here is a situation in which Wikipedia is just the right source:
In probability theory and statistics, the Poisson distribution, named after French mathematician Siméon Denis Poisson, is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant rate and independently of the time since the last event. The Poisson distribution can also be used for the number of events in other specified intervals such as distance, area or volume. For instance, an individual keeping track of the amount of mail received each day may notice that he or she receives an average number of four letters per day. If receiving any particular piece of mail does not affect the arrival times of future pieces of mail, i.e., if pieces of mail from a wide range of sources arrive independently of one another, then a reasonable assumption is that the number of pieces of mail received in a day obeys a Poisson distribution. Other examples that may follow a Poisson include the number of phone calls received by a call center per hour or the number of decay events per second from a radioactive source. (accessed from Wikipedia 23 March 2018).
And, in the present case, the number of adverse coarse particles found in a volume of coating material is also likely to follow a Poisson distribution. This gives the sampling expert just the right weapon with which to offer to evaluate the economics of the suggestion acquisition of the expensive on-line particle analyser.
First, as in every situation in science and industry, the problem should be as clearly defined as possible. In this case the target question can be stated either 1) as the acceptable relative standard deviation of the measurement or 2) as the risk of confidence that the target value 5 particles/ton is not exceeded. This translates into two classical questions:
- How big a sample is needed if a relative standard deviation of 20 % is acceptable?
It is easy to apply the Poisson distribution, because one of its well-known features is that the relative standard deviation (sr) is inversely proportional to the square root of the number of observed events (n):
\[{s_r} = \frac{1}{{\sqrt n }} = 20\% = 0.2\]
From this we obtain that the sample should be so big that it contains n = (1 / sr2) = 1 / 0.22 = 25 particles. At the concentration of 5 particles/ton, this means that the sample size needed is 5 tons! This magnitude was not known to the producer before inviting a sampling expert to evaluate the case. Obviously, this first result made him flinch.
Alternatively, the question can also be stated:
- What is the highest number of large particles in a 1-ton sample that can be accepted to guarantee that the product is acceptable, if a 5 % risk of a wrong decision is acceptable?
From the Poisson distribution we obtain (with a little probability calculus thrown in, not included here) that the probability for 1 particle (or less) is 4 % and for 2 particles (or less) it is 12 %.
So, even a reliable sample, a representative sample of 1 ton will not be able to satisfy the very strict demands here. Besides how to ascertain, to measure the number of coarse particles in such a huge sample? Extreme practical sieving would probably be the only rigorous way—not exactly what was hoped for with an on-line particle analyser!

Paper mill. N.B. The pictured mill is not the one described in the present case history.
In detail, this example shows that even if you buy the most expensive state-of-the-art particle analyser; in this application it would be completely useless—just money wasted. Here is the reason why: particle size analysers are designed to handle samples of the size of ~ a few grams only! Neither is there a sieve system that could separate out just a few 5 µm size particles from tons of fine powder (here one needs to invoke a little standard powder technology competence, which is readily available for the inquisitive consultant, however).
Conclusion
The only way to maintain product quality is to do regular checks and maintenance of the actual production machinery. The only way to study ton-sized samples of this kind of powder material is to build a pilot plant where large-scale coating experiments can be run. While this is indeed an expensive solution, of course, the customer has the same problem. He cannot complain about the quality of the received material based on his own in-house analytical measurements for the exact same reasons. Of course, the customer may well suspect the coating material quality, if there are too many breaks in the paper web after the coating is applied or if the paper maker gets complaints from the printer using his paper, but nothing can be proven with statistical and scientific certitude because of the limitations revealed by thorough application of TOS and classical statistics. The only way forward is to suggest that the producer and the customer together engage in establishing a joint pilot plant for practical systematic testing. It may perhaps be possible to do some fancy down-scaling in this context, but this is another story altogether.
Case 3: The hidden costs—profit gained by using TOS
An undisclosed pulp mill was feeding a paper mill through a pipeline pumping the pulp at about 2 % “consistency” (industry term for “solids content”). The total mass of the delivered pulp was estimated based on the measurement of a process analyser installed in the pipeline immediately after the slurry pump at the pulp factory. Material balance calculations showed that the paper mill could not produce the expected tonnage of paper based on the consistency measurements of the process analyser.
When things became too difficult to proceed, an expert panel was invited to check and evaluate the measurement system. A careful audit complemented with TOS-compatible experiments revealed that the consistency measurements were biased, in fact giving 10 % too high results. The bias originated from two main sources:
- The process analyser was placed in the wrong location and suffered from a serious sample delimitation error (often the weakness of process analysers installed on or in pipelines); the on-line analyser field-of-view (FOV) did not comply with TOS’ fundamental stipulation regarding process sampling, that of corresponding to a full slice of the flowing matter (see, e.g., Reference 2).
- The other error source concerned the process analyser calibration. It turned out that the calibration depended on the pulp quality (never an issue it was thought of at the time of the original calibration: softwood and hardwood pulps need different calibrations).
By making the sampling system TOS-compatible (see all Sampling Columns) and by updating the analyser calibration models, it was possible to fully eliminate the 10 % bias detected.
Payback: It is interesting to consider the payback time for involving the service of TOS in this case. The pulp production rate was about 12 ton h–1. The contemporary price of pulp could be set as an average of $700/ton, so the value produced per hour was easily calculated to be $8400 h–1. The value of the 10 % bias is thus $840 h–1. As the cost of the evaluation study was about $10,000 the payback time of this investigation was about 12 h. To be strict, the costs for the TOS-compliant upgrading of the process analyser should be added, but in this case corresponded to only a few weeks of production (and it should rightly have been covered by the original installation costs).
It does not have to be expensive to invoke proper TOS competency—not at all!
Case 4: The cost of assuming standard normality for serial data
Natural processes and especially manufactured industrial process data are by their nature very nearly always auto-correlated. This is an intrinsic data feature that can be used to great advantage—and at a great disadvantage if not understood and used properly. Thus, a widespread assumption exists that the variation of this kind of serial data can be well approximated by straight forward application of the standard normal distribution. This is a distinctly dangerous assumption, however, that will always lead to sub-optimal (and expensive) sampling plans for estimation of average lot values, at a(ny) given uncertainty level. This case illustrates the consequences of accepting this persistent, but inferior assumption.
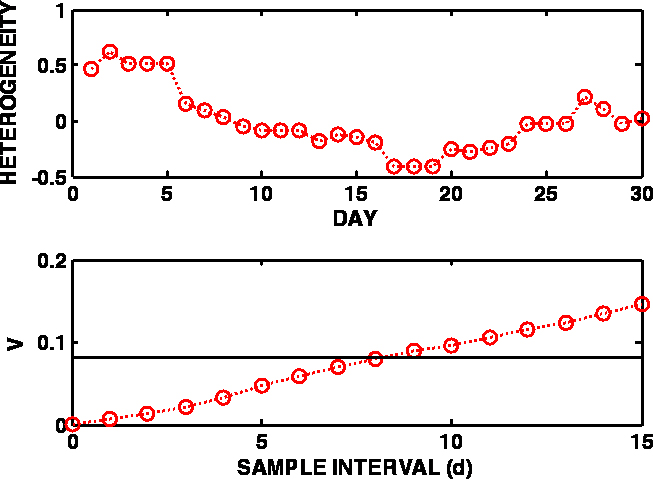
Figure 1. Variation of the sulfur content of a wastewater discharge, expressed as heterogeneity contributions over 30 days (upper panel) and the corresponding variogram (lower panel). The black line in the lower panel represents the overall process variance, i.e. the variance of all 30 heterogeneity values as treated by standard statistics with no auto-correlation considerations.
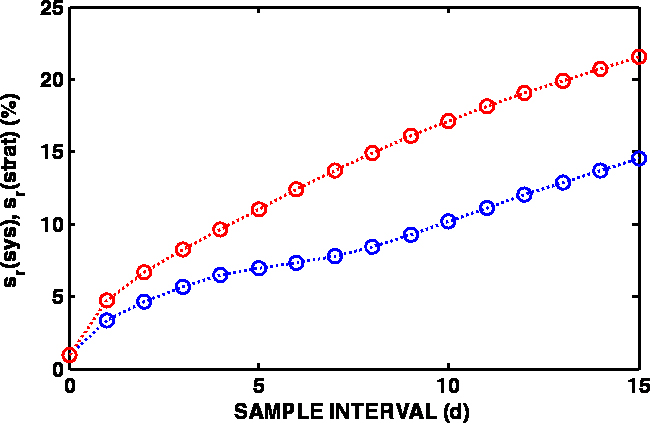
Figure 2. Estimates of the relative standard deviations for systematic (blue) and stratified random (red) sampling as function of the sample lag (one-day intervals).
The data used here are recorded from a wastewater treatment plant discharge point; this data series is used in order to estimate the amount of sulfur that is discharged annually into a recipient lake.
For this purpose, a standard variographic experiment was carried out collecting and analysing one sample per day—for 30 days. Figure 1 shows the process data, expressed as heterogeneity contributions, and the variogram calculated based hereupon. The heterogeneity contribution of a measurement (hi) is defined as the relative deviation from the mean value (aL) of the data series:
\[{h_i} = \frac{{{a_i} - {a_L}}}{{{a_L}}}\]
(see Reference 3 or earlier Sampling Columns dealing with variographic analysis).
The most important aspect of TOS’ variographic characterisation facility is the realisation that the uncertainty of the mean values of auto-correlated series depends on the sampling mode, which can be random (ra), stratified random (str) and systematic (sys) sampling. By analysing the variogram, variance estimates are obtained which subsequently are used to calculate the variance of the process mean:
\[s_{{a_L}}^2 = \frac{{s_{mode}^2}}{n}\]
Figure 2 presents the relative standard deviations as a function of sample lag (multiples of 1d) for systematic and stratified random sampling.
If the normality assumption is used, then the relative variance estimate is the variance estimate calculated from the 30 measurements without any consideration as to their order (their auto-correlation). The relative process variance calculated on this basis is 0.0820, which corresponds to a relative standard deviation sr = 28.6 %.
If, after this experiment, a sampling plan is made with the purpose of estimating the annual discharge using, for example, one sample per week, the relative standard deviation estimates can be obtained from the variogram at sample lag 7; they are 7.8 % for systematic sample selection and 13.7 % for the stratified random mode.
If, instead of depending on a daily sample, say it is decided to collect just one sample per week for the monitoring purpose, then the number of samples in estimating the annual average will be n = 52. Now the following results are obtained:
Relative standard deviation of the annual mean by systematic sampling:
\[{s_{{a_L}}} = \frac{{{s_{sys}}}}{{\sqrt n }} = \frac{{7.8\;\% }}{{\sqrt {52} }} = 1.1\;\% \]
The expanded uncertainty of the annual mean from the systematic sampling is U = 2 • saL = 2.2 %
Relative standard deviation of the annual mean of stratified sampling:
\[{s_{{a_L}}} = \frac{{{s_{strat}}}}{{\sqrt n }} = \frac{{13.7\;\% }}{{\sqrt {52} }} = 1.9\;\% \]
The expanded uncertainty of the annual mean from the stratified sampling is U = 2 • saL = 3.8 %
Clearly, the systematic sampling mode in this case will be the method of choice.
Many current sampling guides still advise to estimate the required number of samples for a targeted uncertainty by using the direct standard normal approximation based on all available data without taking auto-correlation into account. Then the relative standard deviation of the process data will be sr = 28.6 %. If this is used the following will result, if based on the same uncertainty level as for the systematic sample selection:
\[n = \frac{{s_r^2}}{{{{(1.1\;\% )}^2}}} = \frac{{{{(28.6\;\% )}^2}}}{{{{(1.1\;\% )}^2}}} = 678\]
Conclusion
The standard normal distribution assumption is expensive—to say the least! The time used to collect and analyse over 600 extra samples could most certainly be used in a much more profitable way. Knowing well the distinction between a random set of data (for which classical statistics is the correct tool) and a serial set of process data (or similar—it is the auto-correlation that matters) is another element in the tool kit of the competent sampler (process sampler in this case). Variographic characterisation is a very powerful part of TOS.
Lessons learned
(In part, paraphrasing from Reference 4.)
Incorrect sampling and ill-informed analysis generates hidden losses that do not appear in the accountant’s books, for which reason top management do not easily become aware of them.
There is a “natural tendency” to focus on effects, and not on causes of problems. This attitude creates unhappiness, time and money losses, and unfairness while not solving anything.
If one does not fully understand all sources of variability of industrial processes etc., losses are difficult to discover and their economic impacts are difficult to estimate. Yet this quantification is precisely (very often the only) manifestation that top management wishes to see.
When there is little communication between different professions, there is deep trouble. Many professionals are primarily focused on solving their own problems, which are not necessarily aligned with the objectives of the company which is to produce high-quality products at the lowest responsible cost. As a consequence, they do not collaborate well with each other, they do not know each other and each other’s problems well, or at all.
Up to the turn of the millennium, a largely isolated sampling community was unable to communicate effectively the relevance of sampling to top management in economic terms. But for individual consultants the field was wide open. It was a good time for them!
Initiation to the Theory of Sampling has always been considered “difficult” in many sectors in science, technology and industry, because the fundamental texts were often felt to be cryptic, or (quite) a bit too mathematical (for most), and hence not easy for beginners to understand.
However, there has been a revolution is this context in the 15 years since the first World Conference on Sampling and Blending. Today, there is an abundance of easy/easier introductions and texts to be found, the quality of which is excellent. It is hoped that the present Sampling Column is able contribute to drive this development even further. The interested reader will find a continuously updated collection of all Sampling Columns, which contains a wealth of references to the essential background literature at all possible levels at spectroscopyeurope.com/sampling.
References
- P. Carasco, P. Carasco and E. Jara, Eudardo, “The economic impact of correct sampling and analysis practices in the copper mining industry”, in “Special Issue: 50 years of Pierre Gy’s Theory of Sampling. Proceedings: First World Conference on Sampling and Blending (WCSB1)”, Ed by K.H. Esbensen and P. Minkkinen, Chemometr. Intell. Lab. Sys. 74(1), 209–213 (2004). doi: https://doi.org/10.1016/j.chemolab.2004.04.013
- K.H. Esbensen and C. Wagner, “Process sampling: the importance of correct increment extraction”, Spectrosc. Europe 29(3), 17–20 (2017). http://bit.ly/2uf5EGN
- P.M. Gy, Sampling of Heterogeneous and Dynamic Material Systems. Elsevier, Amsterdam (1992).
- P. Minkkinen, “Practical applications of sampling theory”, in “Special Issue: 50 years of Pierre Gy’s Theory of Sampling. Proceedings: First World Conference on Sampling and Blending (WCSB1)”, Ed by K.H. Esbensen and P. Minkkinen, Chemometr. Intell. Lab. Sys. 74(1), 85–94 (2004). doi: https://doi.org/10.1016/j.chemolab.2004.03.013