Jean-Sébastien Dubé, ing. PhD and François Duhaime, ing. PhD
Laboratoire de géotechnique et génie géoenvironnemental, Département de génie de la construction, École de technologie supérieure, 1100 Notre-Dame oust, Montréal (QC), Canada H3C 1K3
Proper sampling of particulate matter for instrumental analysis is a common task in many applied scientific, technology and engineering fields. It is a crucial task for ensuring that measurements made on a given set of samples are representative estimate of the parameters of interest in the original sampling target. Unfortunately, sampling particulate matter is, in many fields, performed without a scientific basis, mostly because its critical role is ignored, or at best, misunderstood, and because of an unawareness of, sometimes a disregard for, the Theory of Sampling. This second part compares grab sampling with composite sampling further illustrating this important issue, again using experience in the field of geo-environmental engineering.
Fix your sampling, not your results
In this second part, we illustrate how measurement variability can be controlled at the sampling stage with a real-world example from a recent study conducted at École de Technologie Supérieure (ETS), Montréal, in partnership with the same consultant involved in the studies presented in the first Part. In this study, we compare the uncertainty derived from grab sampling to that derived from a Theory of Sampling (TOS)-compliant composite sampling process. We here use unpublished results to illustrate a critical distinction which has universal implications: namely that between subjective, purposive or haphazard sampling (i.e. grab sampling) and probabilistic, TOS-compliant composite sampling.
Figure 1 shows lead (Pb) concentration measurements made on samples from a given sampling location in a specific soil parcel using these two fundamentally opposing sampling approaches.

Figure 1. Left: excavated soil at a sampling station. The soil is placed in a longitudinal pile and corresponds to an identifiable layer of a given material (based on visual observation), or to a 50 cm (at most) layer if visual differentiation was not possible. Right: vertical increments are taken perpendicular to the longitudinal axis of the pile and over its total height. The primary sample mass obtained in this manner was approximately 13 kg of dry matter.
By using an experimental design, each approach resulted in several analytical samples in order to assess the various uncertainties involved, sampling vs analytical.
The composite sampling approach unavoidably resulted in larger masses for the primary field samples, which demanded appropriate sub-sampling techniques (in the field or in the laboratory) on the way towards the analytical aliquot. These mass-reduction procedures, and the equipment used, are specifically designed for reducing and eliminating sub-sampling errors. Grab sampling on the other hand does not allow any control on sampling errors. In our study, grab sampling was performed by the consultant company following “usual sampling procedures”. The reader is referred to Boudreault et al.1 for more details on the project, to Gy,2–4 Pitard5 and Esbensen6 for more on the TOS, and to Gerlach et al.7,8 and Petersen et al.9 for more on mass reduction techniques.

Figure 2. Primary samples obtained from the piles shown in Figure 1, which were reduced in the field using fractional shovelling as shown. Each fraction correspond to a final field sample sent to the laboratory. Secondary sample mass thus obtained was approximately 600 g of dry matter.

Figure 3. Left: close-ups of a sample from field fractional shovelling (Figure 2). These samples were brought to the laboratory where they were air-dried and ground (milled) before a first mass-reduction using sectorial rotary splitting (SRS). In the left picture, the maximum particle size is approximately 2 cm. Right: these samples were then milled and ground further before a final SRS step to obtain analytical samples of approximately 1 g of dry matter. In the right picture, the maximum particle size is approximately 200 µm.
Figure 4 illustrates the risks incurred with grab sampling, as also evidenced in the first example above. In practice, only one concentration measurement would have been made and used for decision-making regarding the disposal of this soil parcel. As in the first example, it is still impossible to categorise this soil parcel with any certainty. On the other hand, the TOS-compliant composite sampling procedure yielded much better results—indeed all measurements fall in the same contamination level category. In fact, any of these measurements could have been used to categorise the soil and make a correct decision regarding the fate of this soil parcel.
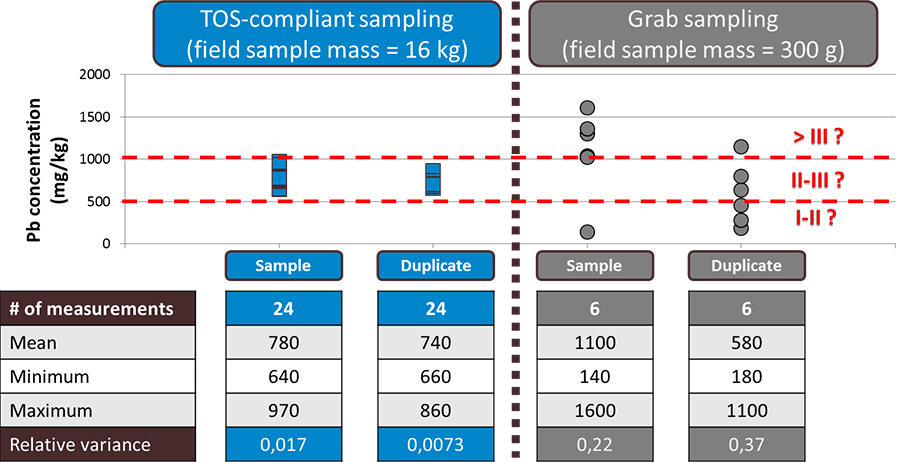
Figure 4. Comparison of uncertainty between TOS-compliant composite sampling and grab sampling based on the effective TSE + TAE. The average relative variances correspond to coefficients of variation of 11 % and 54 % for composite and grab sampling, respectively. There is no doubt which approach is the only acceptable approach for reducing the dominant field sampling errors.
Appropriate reflections in geo-environmental engineering
To what lengths should one go to improve sampling procedures before analysis? This question will often be asked by consultants or soil analysts faced with poor results stemming from incorrect sampling. It is a legitimate question, as changes to the sampling process will reflect on the perceived efficiency of their current operations, performances and reliability.
In the present example, the composite primary sampling required six mass reduction and two comminution steps to obtain an analytical sample, compared to only two mass reduction steps in grab sampling. But, as is clear, ease-of-performance comes at a fatally inflated Total Sampling + Analytical Errors (TSE + TAE), which is never worth risking when lot heterogeneity is significant.
For conciseness, this column will only address the first consideration of any compound sampling operation, the field sampling. The goal is to ensure that all types of particles have a uniform, non-zero probability of being sampled, i.e. compliance with the Fundamental Sampling Principle (FSP).
But things are not necessarily easy in geo-environmental engineering. What is a particle? What differentiates one particle from another? In the TOS, this is described by the constitutional heterogeneity of the soil, which reflects the size and shape of the particles as well as their composition and density. When sampling contaminated soil, for instance, particles can be of geogenic or anthropogenic origin, or both. Thus in general there may be matrix (soil) particles, contaminant particles, as well as matrix particles coated with contaminants. Such a constitutional heterogeneity is complex and difficult to describe in simple mathematical terms. However, to ensure that each of these types of particles is present at each sampling stage during the sampling process, Pitard5 states that “the first rule to fulfil is to ensure that the sample is representative of all the particle size fractions”. Of course the TOS, and Pitard, emphasise that this objective also depends on particle density, but, here Pitard at least provides us with a reasonable starting point. However, even on this basis, geo-engineering encounters problems.
In many fields it is not uncommon for analytical protocols to require that a sample should only have particles smaller than 2 mm, thus leading to the analyst to subjectively remove larger particles, or to screening the sample with a sieve with the appropriate screen size threshold. If the particle size distribution of samples is altered before analysis, the risk of biasing the results is significant.5,6 A crucial aspect of preserving the representativeness of size fractions is identifying the so-called critical size fraction, i.e. the size fraction of high(est) interest—which often also has the highest impact on the heterogeneity (but not always). This target corresponds to the largest particle size(s) in which the analyte is to be found.
However, too often, current sampling guidelines require the arbitrary removal of all large particles under the hypothesis that the smaller particles represent a greater risk to public health. This may, or may not, be true—far from automatically in all cases.
Thus, on contaminated sites, contaminants are also found in large particles of anthropogenic origin, e.g. clinker, slag or associated with particle coatings. Great care must be taken in identifying the critical size fraction for each case individually, since this will determine the minimum sample mass needed to ensure representativeness of particles of equal size, or smaller, than the critical size fraction. This issue is discussed in much more detail in Dubé et al.10
Current geo-environmental guidelines and standards
Geo-environmental engineers and scientists tasked with environmental site assessment currently only have a few cardinal resources for determining minimum sample mass and for selecting appropriate mass reduction techniques. One such leading resource is ASTM Standard D6913 for the determination of the particle-size distribution (PSD) by sieve analysis and its accompanying standard practice C702. D6913 recommends minimum sample mass requirements based on maximum particle size and the number of significant digits for reporting PSD results.
We have previously discussed that the minimum sample mass requirements in D6913 are not compliant with TOS principles, but rather defer to practical requirements to avoid sieve overloading or for composite sieving. And also D6913 fails to address the constitutional heterogeneity of the soil and the critical size fraction properly, but rather seeks to adapt the sampling process to existing equipment, which obviously will fail. Therefore, the minimum mass requirements in D6913 actually lead to significantly larger variability in analytical results than expected.10
ASTM D6913 and C702 also prescribe the use of mass reduction techniques for the procurement of the sample for traditional analysis. Riffle splitting (RS) is recommended for dry flowing soil, while coning and quartering (C&Q) and miniature stockpile sampling (MSS) are suggested for moist soil. However, D6913 and C702 do not justify these recommendations based on performance data or any other evidence. Analysing their performance and comparing them for their recommended use, i.e. RS for dry soil versus C&Q and MSS for moist soil, may also be misleading. For moist soil, sampling variability significantly decreases due to matrix moisture and increased coherence and hence reduced segregation.10 Therefore, a sampling method which performs apparently well on moist material, could perform very poorly on dry material. Petersen et al.9 have observed that splitting methods outperformed shovelling methods for dry materials. Moreover, Pitard5 and Esbensen6 strongly advise against the use of coning and quartering and miniature stockpile sampling (also called degenerate fractional shovelling).
Discussion and conclusions
The present exposé, Parts 1 and 2, focuses on how incorrect primary and secondary sampling can severely affect the quality and validity of analytical measurements made on the resulting aliquots. The context of soil sampling in environmental site assessment was used to illustrate several critical issues related to practical sampling before analysis. We have also emphasised that all size fractions in the sampled particulate matter must be proportionally present in any sample thereof, lest all hopes for representativity be lost.
It was seen that it is not a straightforward matter simply to rely on current guidelines and standards. Most, sadly, ignore the TOS, at their peril, and even provide recommendations which violate its principles. Unknowingly, the analyst will then make measurements on samples which are not representative of the initial lot to be characterised.
Because of such general lack of awareness of the TOS, it is also difficult for analysts to understand their role with respect to the representativeness of the measurement data. Their focus is largely on the final measurements in the laboratory, but their work manifestly includes sub-sampling to reduce the mass of particulate matter so as to comply with the inherent volume/mass requirements of the analytical instrumentation. In environmental site assessment, analysts are de facto an essential part of the whole “from-lot-to-aliquot” pathway, as they at least perform the necessary last mass reduction, which represents a minimum of two orders of magnitude of mass reduction—and which at times often also involve a highly subjective removal of “larger particles”.
The first parts of the full sampling-and-analysis process occur in the field and are often performed by the consultant’s field technician. This gap in the “chain of custody” of the sampling process between the consultant and the laboratory is particularly problematic, especially as much as the current incorrect sampling practices are left without a clear responsibility. No one takes full responsibility for the representativeness of the complete sampling process in such circumstances. A possible solution would be that a single responsible agent, knowledgeable in the TOS, should design, perform and ultimately be responsible for the whole sampling process until analysis. Analysts would then only receive representative test portions, aliquots, ready for analysis and would, therefore, be able to fully take responsibility for the quality of their measurements, i.e. the true TAE, while the responsibility for quantifying all sampling and sub-sampling uncertainties before the analytical aliquot (TSE) would also have been clearly described and assigned.
Technically, the conclusion from the above two, out of many similar studies, is that composite sampling at the primary sampling stage is imperative and should be mandatory for all significantly heterogeneous materials that cannot be subject to mixing. The necessary additional crushing and sub-sampling stages, which will vary significantly as a direct consequence of the material heterogeneity encountered, are simply the price to pay for documentable primary sample representativity without which the raison d’être of analysis has disappeared: what could be the reason for analysing a sample (or a derived aliquot) that is known to be non-representative? None. There is no such reason.
There are no shortcuts to representative sampling! Composite sampling must always be used, as this is the only available guarantee for representativity of significantly heterogeneous materials. Contaminated soil is an excellent basis upon which to demonstrate these essential truths because of its often dramatically complex nature.
Factbox
Below, we present performance results for the mass reduction methods recommended by D6913/C702 and compare them to fractional shovelling and grab sampling. ASTM 6913 only recommends RS for dry soil, but for reasons discussed above, all methods were compared using only dry soil here.
Figure 5 shows the expanded uncertainty (k = 3) for the particle size distribution (PSD) obtained for each method on the same soil. As expected, RS performs better than the other shovelling-based methods. Amongst the latter, fractional shovelling performs better than C&Q, while MSS is approximately equivalent to grab sampling and thus performs almost as poorly.
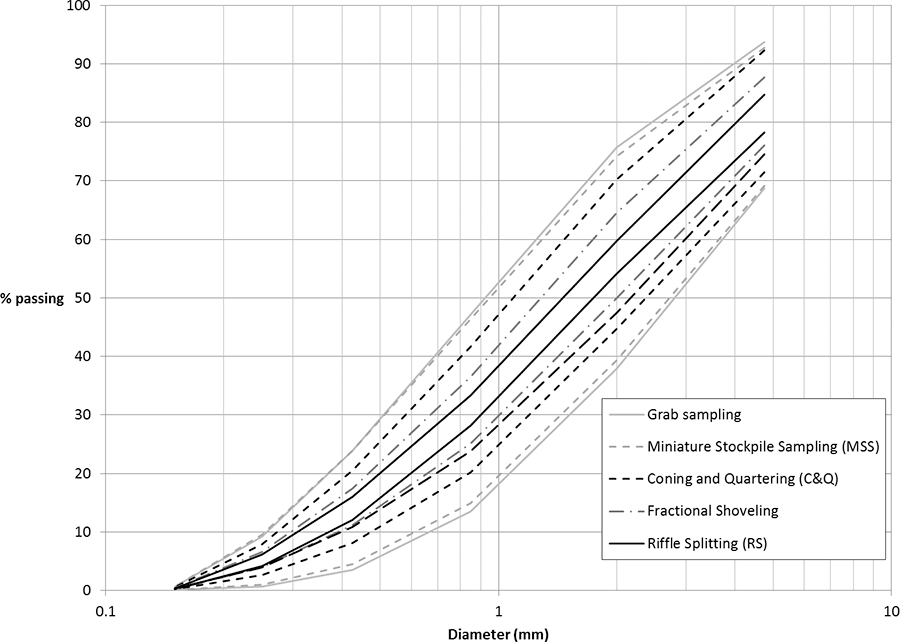
Figure 5. PSDs of a comparison soil obtained using three sampling techniques recommended in ASTM 6913 (MSS, C&Q, RS), fractional shovelling and grab sampling.

Figure 6. Soil corresponding to the PSD results shown in Figure 5. The laboratory bench pile shows a distinct constitutional and size heterogeneity manifestation. In this picture, it was undergoing sampling using MSS as defined in ASTM D6913. Samples were obtained by combining three increments grabbed from subjectively selected spots on the pile. The resulting sub-samples are seen in the metal plates in the top-right corner.
Acknowledgements
The authors thank Jean-Philippe Boudreault and Laurent Nolak.
References
- J.-P. Boudreault, J.-S. Dubé, M. Sona and É. Hardy, “Analysis of procedures for sampling contaminated soil using Gy’s Sampling Theory and Practice”, Sci. Total Environ. 425, 199–207 (2012). https://doi.org/10.1016/j.scitotenv.2012.03.013
- P. Gy, “Sampling of discrete materials—a new introduction to the theory of sampling I. Qualitative approach”, Chemometr. Intell. Lab. Syst. 74, 7–24 (2004) https://doi.org/10.1016/j.chemolab.2004.05.012
- P. Gy, “Sampling of discrete materials II. Quantitative approach—sampling of zero-dimensional objects”, Chemometr. Intell. Lab. Syst. 74, 25–38 (2004) https://doi.org/10.1016/j.chemolab.2004.05.015
- P. Gy, “Sampling of discrete materials III. Quantitative approach—sampling of one-dimensional objects”, Chemometr. Intell. Lab. Syst. 74, 39–47 (2004) https://doi.org/10.1016/j.chemolab.2004.05.011
- F.F. Pitard, Theory of Sampling and Sampling Practice, 3rd Edn. CRC Press, Taylor & Francis Group (2019). https://doi.org/10.1201/9781351105934
- K.H. Esbensen, Introduction to the Theory and Practice of Sampling. IM Publications Open (2020). https://doi.org/10.1255/978-1-906715-29-8
- R.W. Gerlach, D.E. Dobb, G.A. Raab and J.M. Nocerino, “Gy sampling theory in environmental studies. 1. Assessing soil splitting protocols”, J. Chemometr. 16, 321–328 (2002). https://doi.org/10.1002/cem.705
- R.W. Gerlach, J.M. Nocerino, C.A. Ramsey and B.C. Venner, “Gy sampling theory in environmental studies: 2. Subsampling error estimates”, Anal. Chim. Acta 490(1–2), 159–168 (2003). https://doi.org/10.1016/S0003-2670(03)00568-3
- L. Petersen, C.K. Dahl and K.H. Esbensen, “Representative mass reduction in sampling—a critical survey of techniques and hardware”, Chemometr. Intell. Lab. Syst. 74(1), 95–114 (2004). https://doi.org/10.1016/j.chemolab.2004.03.020
- J.-S. Dubé, J. Ternisien, J.-P. Boudreault, F. Duhaime and Y. Éthier, “Variability in particle size distribution due to sampling”, Geotech. Test. J. 44(1), 26 (2021). https://doi.org/10.1520/GTJ20190030

