D. Aldwin Vogela and Kim H. Esbensenb
aTechnical & Quality Director, Commodities Global Service Lines, Bureau Veritas, Rotterdam, the Netherlands. commodities.bureauveritas.com
bIndependent researcher, consultant, owner, KHE Consulting, Copenhagen, Denmark. kheconsult.com. Adjunct professor, Aalborg University (AAU), Denmark; Adjunct professor, Geological Survey of Denmark and Greenland (GEUS); Professeur associé, Université du Québec à Chicoutimi (UQAC), Québec; Guest professor University of South-Eastern Norway (USN); Guest professor Recinto Universitario de Mayaguez, Puerto Rico
DOI: https://doi.org/10.1255/sew.2021.a16
© 2021 The Authors
Published under a Creative Commons BY-NC licence
This cannot be true—surely sampling and weighing are different activities. Well yes—and no! Sampling and weighing of traded metal, mineral and agro commodities are different activities—but at one or several stages in the supply chain they will come together in a single focus point, which is value ($, EUR). The commercial value of bulk commodities depends on two factors, quality and quantity. As an example, a shipment of iron ore with a certain certified weight cannot be traded without a reliable declaration of its quality, iron percentage. Similarly, a shipment of rice (assuming pure rice with no contaminants) cannot be paid for without its certified weight. At least once in all supply chains, someone in treasury will look at the final output of what has to be assumed is the result of diligent representative sampling and reliable weighing. But the final accounting will not show the overall accuracy and precision of sampling, preparation and analysis, and neither show the accuracy class of the weighing device. In the final accounting, this will all be the same for the user: what is important is the monetary value that is to be paid or received. The demands for minimisation of both sampling and mass determination errors are often hidden, but absolutely critical. This column specifically focuses on weighing errors in more detail, adding essential theoretical elements and practical know-how to the framework of the Theory of Sampling.
Quality and quantity—equal factors
In the world of commercial sampling of commodities this is nothing new. Historically, this was one of the driving forces why Pierre Gy started to address the fundamental conceptual and theoretical issues and the critical practical problems in sampling. Gy started to investigate the quality issue in earnest in his first assignment in 1946 in the then Belgian Congo, when he started out working as a research engineer for the mining and processing trade organisation Minerais et Metaux.1–3
Gy realised that sampling of bulk particulate materials is a challenging combination of understanding the concept of heterogeneity and mastering the appropriate engineering principles involved, which many at the outset would believe could be significantly helped by statistics. After all, the term sampling is for very many (individuals, organisations, academic disciplines etc.) a statistical term. However, it turned out that statistics, based on analytical results, by itself would not deliver the solution to how to optimise sampling procedures and equipment when facing heterogeneous materials. Gy’s monumental theoretical analysis, developed over the next 25 years revealed the need for a set of sampling errors which are not all of the traditional statistical type, systematic vs random errors. In particular, Gy’s analysis uncovered bias-generating errors caused by the interaction of material heterogeneity and ill-reflected sampling procedures that had to be dealt with in a more comprehensive manner.4,5 But statistics does play a role in the Theory of Sampling (TOS), which manifests itself in the fact that numerical determination of the quality factor is an estimation, an estimation of the composition of a lot.6
But what about determination of the quantity of a lot, i.e. the weight of a lot? This is the subject matter covered in this column.
Representativity—at the centre of everything
A critical issue is: what are the criteria that need to be satisfied for a compositional estimation to be declared “representative”? Is it enough that certain error tolerances of the quality and quantity of an analytical aliquot are suitable for the needs of the person that will use it; for contractual purposes, for example? There is a practical side to this issue as well, one that has prompted introduction of the term “fit-for-purpose representativity”.
With the TOS as a guiding framework,6–8 it turns out that these issues are rather intertwined, but fully resolvable. Assuming that the specific analytical method used can be relied upon to be “in statistical control”, i.e. the analytical process is accurate and precise according to universally agreed upon characteristics, a condition well complied with by all the world’s scientific, technical and commercial analytical laboratories. Then, in order for the analytical determination to be representative, it is necessary-and-sufficient that both the analytical aliquot, as well as the previous multi-stage samples and sub-samples, are all representative of the primary lot material.4,5
This understanding is one of the TOS’ greatest achievements, that the entire “from-lot-to-aliquot” pathway is causally connected to the analytical determination and whether analytical results can correctly be considered representative, or not. In fact, the TOS stipulates that there is no characteristic of a sample itself that can vouch for its status—only the status of the entire sampling pathway is able to pass judgement on whether the test portion is representative or not. Thus, in a very direct sense, analytical results depend on the full “lot-to-aliquot” pathway—which can be representative but certainly also not, ibid. It matters very much that managers of analytical laboratories and Testing, Inspection, Certification (TIC) companies are aware of this critical connection; this context is described in depth in References 9 and 10.
However, at this point we may have already lost the interest and attention of the treasury department.
Treasury: “Estimation? ... Error tolerances? ... Representativity? So what? The monetary value on the invoice is all that matters and the commodity will not change because of all that.”
How correct—and how wrong at the same time!
Money rules the world—it is often claimed
The commodity does indeed not change in and of itself (loss, theft or damage excluded), but what if the analytical sample was not representative of the original lot, which it is always tacitly assumed to represent without ambiguity? This is the raison d’etre for the TOS.
If so, the invoice value will actually vary and be different if the commodity is sampled and tested at two or more TIC locations, e.g. loading port vs discharge port, or similar scenarios: lab 1 vs lab 2; buyer vs seller. Why? Because lot materials are always heterogeneous, a sampling bias will always ensue if all sampling operations involved in TIC are not representative. Thus, based on the TOS’ 70+ years’ experience, without guarantee for representativity, analysis of heterogeneous lots at two locations will assuredly always lead to dissimilar analytical results … and this ambiguity will only proliferate were additional attempts tried with the purpose of checking whether the sampling bias is constant. However, according to the TOS this can never be.5,6
This is the point where we are absolutely sure to lose the treasury department:
Treasury: “The same lot, characterised at two ports, will always give rise to dissimilar analytical results? Always?” The treasury department, and/or the trader (commodity trader), will now likely hedge: “OK then, yes sure, this may be so, but we have the appropriate technical staff to take care of all this sampling”.
However, what about weighing—in what sense can this be “the same as sampling”?
Sampling vs weighing
Well, weighing is also an act of estimation when weighing is carried out on an industrial scale as, for example, with traded bulk commodities. The question for weighing is, as with sampling: how representative shall it be? How accurate shall the mass determination have to be? Ultimately, within the weighing domain there are in fact both incorrect and correct weighing errors, in perfect analogy to the domain of sampling! To be demonstrated below.
Sampling errors: a breakthrough concept
Pierre Gy was able to come to grips with the reasons for non-representative sampling; there are several reasons.4,7 He identified and analysed in detail the consequences of both unmitigated Incorrect Sampling Errors (ISE) and Correct Sampling Errors (CSE). The ISEs are:
- Incorrect Delimitation Error (IDE)
- Incorrect Extraction Error (IEE)
- Incorrect Preparation Error (IPE)
- Incorrect Weighting Error (IWE)
ISEs are responsible for creating a sampling bias, which must be avoided at all costs.11 Below, we exemplify all these types of ISE in the weighing domain.
Weighing Incorrect Delineation Error (wIDE)
In sampling, avoiding IDE is all about strict reproducibility in delineating incremental cuts in a correct fashion, e.g. being able to take a full core from top to bottom in a stockpile (all the way to the bottom), or taking a complete plane-parallel cross-section across the full material stream on a moving, or stopped, conveyor belt.
In weighing there are similarities when it comes to correctly delineating the mass that is weighed.
An example from the weighing domain would be a weighing device that gradually moves away from its calibration condition: measurement “drift”. This is often the largest attributor to a weighing bias. If not properly trained, the operator of the weighing device is often not aware of this, but strongly believes that it is sufficient just to observe the service interval between calibrations prescribed in the manual accompanying the acquisition of the device. With industrial weighing devices, such as belt-scale weighers, there are many variables that each will have an impact on the device drifting further and further away from its last state of validation.
The analogy in the sampling domain is like not being able to observe the development of the crooked and contorted edges of a cross-stream sample cutter, Figure 1. In both cases a non-constant IDE is gradually developing, but this non-constant bias is hidden from view.

Figure 1. Falling stream cutter with contorted edges that result in incorrect delineation (IDE).
The following is a list of salient IDEs associated with a belt-scale weigher (Figure 2):
- Change in belt length: because the physical belt material stretches over time
- Change in belt tension: because of neglected checks and service of tensioners
- Change in drum diameters: because of poor cleaning causing dirt between drum and belt
- Mis-aligned weighing idlers: because of slacking of the belt
- Slipping and/or dirt coverings of the speed sensor
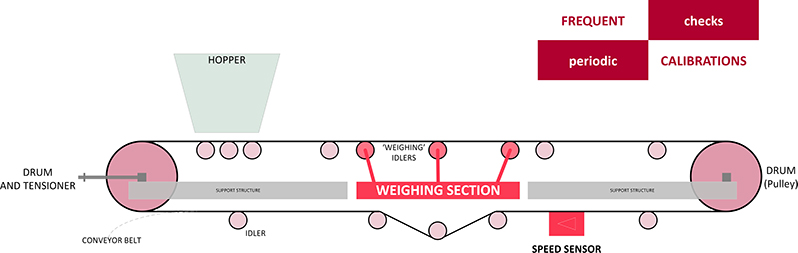
Figure 2. Principal set-up and key parts of a belt-scale weighing device.
Weighing IDEs must be eliminated to avoid bias, exactly as in the sampling domain. This is fully possible through frequent, or continuous, inspection and diligent maintenance of the mechanical weighing system, which would be proper diligence, more conscientious than just referring to the calibration validity sticker—if there is such a thing in the first place! It is all about inspection and maintenance here, about frequent checks and verifications. Above all, it is about proper training of the personnel involved—and not only about weighing, the full TOS framework needs to be in mind.
Calibration: operation that, under specified conditions, establishes a relation between the quantity values with measurement uncertainties (provided by other/known measurement standards and corresponding indications with their known measurement uncertainties).
Verification: provision of objective evidence that a given item fulfils the specified requirements.
Weighing Incorrect Extraction Error (wIEE)
In the sampling domain, one is committing an IEE if not all of the (correctly) delimited cut is actually extracted. In the weighing domain this means that not all material is weighed even though it has been correctly delimited.
It is instructive to perform a “thought experiment” for weighing trucks over a weighbridge (Figure 3). Of course, interest is not in the mass of the trucks themselves, but specifically only in the mass of the cargos. For correct “extraction” of the mass, i.e. the correct determination of the weight, the requirement is, therefore, to weigh the truck twice: full and empty. The delimited difference between those two weighing results constitutes the cargo mass.

Figure 3. Full (container doors closed) container on truck: gross mass. After discharge, the empty container (doors open), the truck is weighed again: tare mass. The difference will be the cargo mass.
The weighing IEE, wIEE, crops up as a consequence of an attempted logistical shortcut during practical cycling of loading or discharge operations in a port, where the same trucks are used to transport a commodity over a relatively short distance. The wIEE originates here with the unfounded assumption that the mass of a specific empty truck is constant within a bracketed time frame and a within a well-defined specific port footprint. But it is not unheard of that the “burden” of weighing is reduced by only passing laden trucks over the scale and using the empty truck mass for more than one “trip” from storage to weighbridge to quayside and vice versa… or rather not vice versa, but proceeding straightaway to loading again. This means weighing any “unextracted” cargo remnant mass twice over, for example all of the two tons as seen in Figure 4 (right panel). The value of two tons of this specific material corresponds to EUR 2500; a shipment may consist of ~400 truckloads. One may imagine this to happen, say for every every fifth truck—with the result of EUR 200,000 worth of weighing error. The point here is also that this type of wIEE may not necessarily occur with any regularity with obvious consequences.

Figure 4. Left: Trucks moving in a port area from storage, via a weighbridge to quayside for discharge (v.v.). Right: Truck tipping cargo at quay for loading onto a receiving vessel. Inside the yellow circle 2000 kg of cargo remnants are visible that will remain inside the truck during its next trip (wIEE).
So far, the above “two out of two” signifies that certain ISE have direct counterparts in the weighing domain (IDE, wIDE; IEE, wIEE).
What about IPE (or IWE)?
The IPE, however, is an issue where there is no easy comparison, simply because there is not much to “prepare” in the weighing domain—and drawing a parallel with electric current fluctuations and its impact on the load cell signal and its calibrated value in kilograms may be more than a bit farfetched.
But there are occasions in which a critical but sometimes unrecognised IPE in the sampling domain, evaporation of moisture (loss of moisture), may have an analogue in the weighing domain. In both domains this takes the form of unrecognised, uncontrolled or unmitigated loss of moisture which is actually determined as weight differences. The classic example is a primary wet sample having to comply with a logistical waiting period in a dry environment before being transported to the central laboratory—but left in a container without a waterproof lid in high ambient temperatures. This scenario depicts unrecognised moisture loss that will interfere with subsequent moisture determination, which structurally will always be too low by an unknown proportion. This clearly leads to an inconstant, significant sampling bias (N.B. there are also other “agents” at work in the IPE domain; the above is not a comprehensive treatment.)
Moisture is a key parameter in most commodity trade TIC protocols, where similar mishaps may occur if sufficient professional competence is lacking. Perhaps the easiest way to cover all such possibilities is to focus on the time intervals in question, i.e. the time duration in which wet samples may unwittingly lose moisture, partially or completely. A disconnect between time and place of sampling and time and place of weighing is clearly a sampling error. [There is a close connection to the topic “error” vs “uncertainty” presented and discussed in the preceding column,12 in which can also be found an example of a strict parallel w.r.t. a mismatch error (disconnect) between the acquisition locations of spectra and reference samples [X,y] in a multivariate calibration data analytical context.] As a graphic example: what is the meaning of weighing a commodity of gold concentrates, packed in big bags, at the time when the consignment is loaded into the cargo holds of a container ship … when this is in fact ten days (10) after the “freshly filter-pressed concentrate” was sampled (following all the necessary principles in the TOS) during filling of the bags at the refinery plant. Unavoidably, some moisture will have seeped out of the bags in the 10-day interval prior to weighing, but how much? And was the moisture loss of similar magnitude for all bags? The mass of this moisture obviously should have been weighed at the same time as—and thus complementing—the compositional sampling! Somebody, or some protocol, is manifestly responsible—hence we are dealing with a sampling error, in this case a logistical error, an error that could and should have been avoided. Whether this scenario should be considered as a “classic” IPE or as a weighing IEE (wIEE) does not really matter. Either way, it is of critical importance to be in command of enough TOS and practical weighing competence to understand the manifest need to eliminate such an error, as no type of subsequent correction is ever possible.
ISE: Weighting
This topic may appear a little complex: please pay close attention to the letter “t” as what follows is about a technical weigh-t-ing error in weighing. Again, use is made of a belt-scale weigher as an example, not because they are flawed by design, but because they are very often used incorrectly—and they make for a particularly clear demonstration.
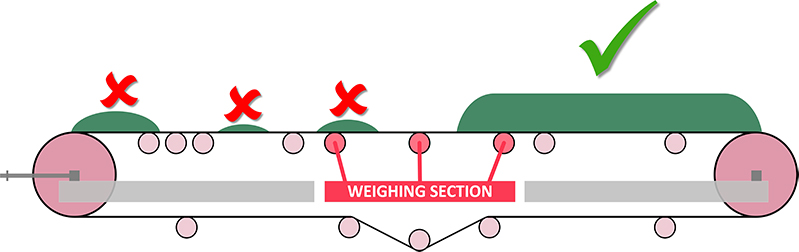
Figure 5. Left (with error marks): Incorrect loading of the belt resulting in too low weight signal. Right (with correct checkmark): Correct, uninterrupted loading of the belt resulting in weight signal as designed.
Figure 5 shows what is happening when mass is supposed to be determined by weighing, but without considerations of potential pitfalls. For an accurate mass determination to be possible, there must be a certain minimum load on the belt-scale weigher. If not, the tension of the (mostly) empty belt will prevent the downward force exerted by the “spotty” material stream on the belt to be registered by the load cell(s) in the weighing section. It is, therefore, important that the on-belt loading rate during cargo handling operations is properly controlled at all times, also during start-up and close to termination. On-belt loading rates should be constant as much as practicalities allow, so as to result in a steady state on-belt material steam (constant material flux). Operators of front-end-loaders that pile cargo onto the belt, crane operators that grab cargo from the holds of a vessel should be properly trained and well aware of this pertinent minimum load requirements of the weighing device. For professional work, it is unacceptable to let cargo “trickle” onto the belt for long(er) periods of time as the mass(es) involved will be underrepresented. Its proper mass(es) will go unnoticed. This is clearly a technical weigh-t-ing error—which unavoidably creates a weighing bias to be avoided “at all costs”. Somebody will clearly have to pay for the un-weighed mass(es), but whether this is the buyer or the seller is equally unacceptable from a professional TIC point of view. The responsibility of the TIC certification mandate is to eliminate this kind of unnecessary wISE.
Correct Weighing Errors …
Treasury: Sorry, what? “Correct … Errors, how can an error be correct?”.
The reader is referred to Gy’s original definitions of correct vs incorrect errors.5,10 In the sampling domain, CSEs can never be completely avoided as they are a function of the interaction between the quality variation of a heterogeneous lot and the sampling process with which increments are selected and extracted in practice. Any estimated sample composition, and hence also of the estimated lot composition, will inevitably show a difference with respect to the true lot value.1–6,11 The magnitude of this CSE (most often it is the sum of the Fundamental Sampling Error and a residual Grouping and Segmentation Error) needs to be managed by first setting an acceptable CSE target threshold and then designing a sampling plan in which the number of primary increments (Q) is the key parameter with which to make the total CSE in compliance—for significantly heterogeneous materials, more TOS facilities may also have to be used. This is where the full TOS framework must be at the disposition of the operator, supervisor, CTO …
But in most weighing scenarios of bulk commodities, the whole cargo must be weighed. The situation here often is that what the properly managed, meticulously calibrated and well-maintained weighing instrument shows… is the true weight. But this is based on a wrong assumption, as will be explained.
For determination of cargo mass there are sometimes occasions where a standard statistical sampling is required, for example regarding weighing shipments of bagged rice where a certain number of these bags are the only ones actually weighed. The corresponding average result is then multiplied by the tally of the whole number of bags in the bag population. Most sampling and weighing operations are relatively “easy” for commodities showing up in this manner of conveniently bagged volumes/masses.
ISO standards, such as ISO 12743, provide examples of overall targets for desired CSE magnitudes. Remember that at this stage it is traditionally assumed that all bias-generating errors (ISE) have indeed been eliminated (a very convenient assumption). But, assumptions are not always right….
Food for thought: A target value for standard deviation of nickel determination may be, say, 0.2 % (absolute). With precision at 95 % confidence, roughly twice standard deviation gives us a target of 0.4 %, IF all incorrect errors have indeed been removed, all that remains is precision only. Weighing Standards such as issued by OIML (Organisation Internationale de Métrologie Légale/International Organization of Legal Metrology) and NIST (National Institute of Standards and Technology, USA) are manifestly based on this fundamental assumption that there is no bias. Confusingly, however, these weighing reference standards still speak of “accuracy class” and not “precision class”. “Accuracy classes” are decided upon according to the number and the value of scale divisions of the pertinent weighing devices. This means that the accuracy of a scale is dependent on a value expressed in a unit of measurement (e.g. kilogram) between two consecutive division indications. Let’s again take the weighbridge as an example: most weighbridges are of OIML or NIST accuracy Class III, which means they have between 500 and 10,000 scale divisions. So, for a Class III weighbridge of 50,000 kg capacity and 500 scale divisions, the smallest unit indication is 100 kg. For another Class III weighbridge of 50,000 kg capacity but 10,000 scale divisions, the similar unit indication is 5 kg. It is very clearly not accuracy that is discussed here, but precision—QED.
Augmented TOS insight: The number of scale divisions in the weighing domain is what the number of primary increments is in the sampling domain! The higher the number of scale divisions, the more precise the weighing will be. It will perhaps not come as a surprise that the price of a weighing instrument shows a clear correlation with the number of scale divisions it provides. This situation prompts some wondering at the all-important treasury department…
“Wow”, so the inexpensive, yet contractually binding Class III weighbridge at our receiver port in Houston, TX, can have a 20 times greater error than my own expensive weighbridge in Rotterdam with its “superior” 10,000 scale divisions?” Well yes, but this is not all… The precision target for Class III weighing devices may be about more than just scale division. The Maximum Permissible Error (MPE) for Class III weighing devices according to OIML can be three (3) scale divisions; while for NIST Class III it can be up to five (5)! [For readers not in full TOS command, apologies for a slight possible confusion here, as MPE is also known as the acronym for Minimum Possible Error. However, from the specific context there is never any serious misunderstanding possible; the latter MPE applies to variographic analysis, while the former MPE pertains to weighing exclusively; if necessary the terms MPEvariographics vs MPEweighing can be used.]
Treasury: “What? So my container that was weighed as 39,500 kg may have had a MPE of 60 kg here in the Netherlands, but our recent dispute, where the container was weighed for payment in the USA as 39,000 kg, could just have been a result of the MPE of 500 kg ‘over there’?”
Well yes, but wait, there is still more! Remember that for proper determination of cargo mass, one actually needs to weigh the container twice: as full and as (assured) empty. Consequently, one will then need to consider MPE twice…. Keep your weighing balance sheet flexible!
All this potential confusion (if you are not a very experienced, indeed a chartered operator) is all for scales that has the same accuracy class on their treasured calibration certificate, but which in reality are not identical in practice. And the present initiation to the weighing domain has not even looked at different types of weighing instruments and different accuracy classes yet!
Minnitt hit the nail on its head when he stated:13 “The costs of sampling installations and new equipment are usually hard for management to accept because the adverse effects of poor sampling practice never appear on the balance sheet. The mining industry is replete with stories about the adverse effects of trying to save money on sampling equipment and installations.”
To which the present authors would like to add: “Sampling and weighing are the same type of criticality for more fully transparent balance sheet and final report information”.
MPEweighing is a Correct Weighing Error and should be given the same attention as a Correct Sampling Error!
Weighing along the mine-to-loading port- to-cargo-to-discharge port-to-balance sheet
Here is a way to try to express the cost of weighing imprecision as a result of different devices available at the principal locations along the commercial TIC pathway. It is a thought experiment of weighing a commodity along the full supply chain from mine to terminals and ports to its destination. For this demonstration we make use of a commodity parcel which is prescribed a precise weight of 5000 tons—it is not the weight per se that is of interest, it is the deviations from this nominal weight it experiences on its merry way. This parcel is, furthermore, completely oblivious to changes in moisture a.o.—not a gram of moisture was lost in transit, and not a kilo was picked up as dirt (no IPE). But the commodity was weighed with the different devices and methods in use at the principal locations shown in Figure 6, each with their own precision characteristics. The magnitude of imprecision is expressed by the length of the whiskers extending from each estimated mass (±2 std).
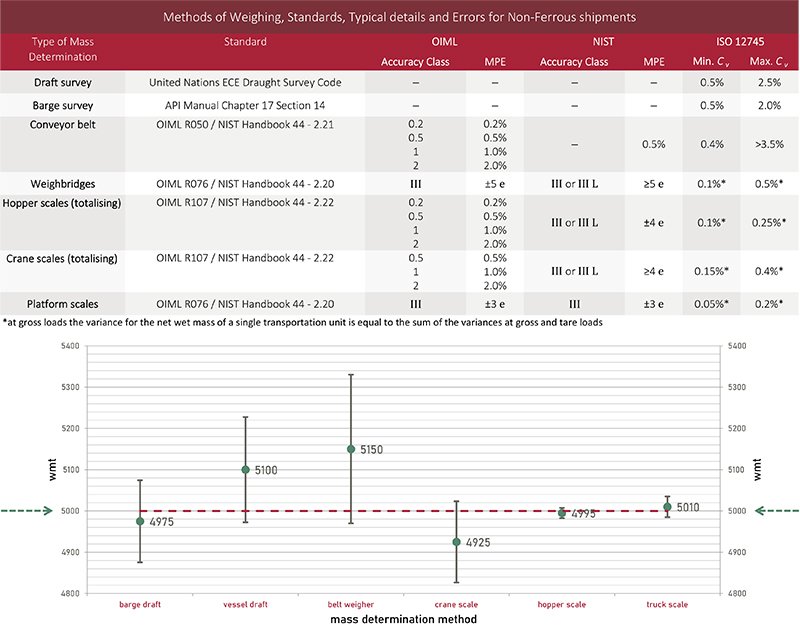
Figure 6. Top: Table with methods of weighing and interpretation of precision (MPE and Coefficient of variation). Bottom graph: Visual representation of mass estimations and precision “whiskers” of different weighing methods on the same nominal 5000 tons cargo.
Each weighing method estimated the mass of the commodity according to appropriate manuals and standards, and importantly, MPE was not exceeded anywhere. Yet the maximum difference between six weighing methods, all used appropriately and in full compliance, was no less than 225 metric tons. This is an example slightly on the extreme side, but fully realistic. In this context, using the same commodity as in the wIEE example above (EUR 1250/ton), some trading entity would have unnecessarily lost or gained the equivalent of EUR 280,000 depending on which weight estimate was used. Far from trivial in commodity trading… and great for the present didactic demonstration.
The lesson is clear: there is sampling expertise (use it well), and there is weighing experience (use it well)—and your TIC partner better be fully competent in both aspects. Sampling and weighing are two sides of the same TIC coin.
Sampling and weighing—different but the same…
Based on Reference 14: “From the early conceptual stages of designing logistics of a port or terminal where sampling and weighing is needed, all the way to manual sampling for lack of other options, expert advice should always be taken to ensure that:
- Proper unrestricted ‘access’ is available for correct sampling equipment [the TOS’ Fundamental Sampling Principle must be complied with, at all times and at all locations].
- Sample mass and frequency are ‘selected’ in accordance with the specific heterogeneity characteristics of the material vs the desired risk for being wrong.
- Sampling increments, or cuts, are taken by a properly designed and maintained plan that assuredly will ‘include’ all particles of the lot without changing the commercial characteristics in any of the subsequent processes leading to the final portion that is tested.”
The parallel with weighing:
- There is a proper location and an appropriate instrument for correct weighing.
- Accuracy class and scale divisions are “selected” in accordance with the specific material properties—price!—vs the desired risk for being wrong.
- Weighing follows a properly designed and maintained plan that will ensure that all particles of the lot will be weighed; nothing is added, nothing is lost.
Conclusions
This column only offers an initiation to the domain of weighing as a critical complement to the sampling domain; this column presents critical elements for an augmented TOS framework.
It would appear that in the weighing domain most attention is given to the technology involved, i.e. to weighing devices and their installation, and to calibrating and verification (most likely carried out during commissioning), while often neglecting their true design objectives and especially the actual performance during long(er) lifetimes in action where “better-safe-than-sorry” checks and inspection are of critical importance. Compare with the sampling domain, where focus all too often is overly on analysis s.s. and very often focused on Measurement Uncertainty (MUanalysis), to the neglect of the full complement of possible sampling and sub-sampling errors that manifestly all reside in the before analysis domain.
Typical weighing domain errors (wIDE, wIEE, MPEweighing) were introduced and illustrated with the intent to augment the TOS’ framework. The TOS is the only guarantee for sampling representativity due to bias that could have been avoided and precision that could have been achieved. The analogue scenario in the weighing domain concerns an unnecessary loss of trust w.r.t. certified weight declarations.
Since (in the context of the present discussion) “value” = representative “composition” × unbiased “mass”, sampling and weighing are both different, and the same… Thus, the final outcome of sampling and weighing marry each other and merge into the same commercial unit of measurement: value, Figure 7.
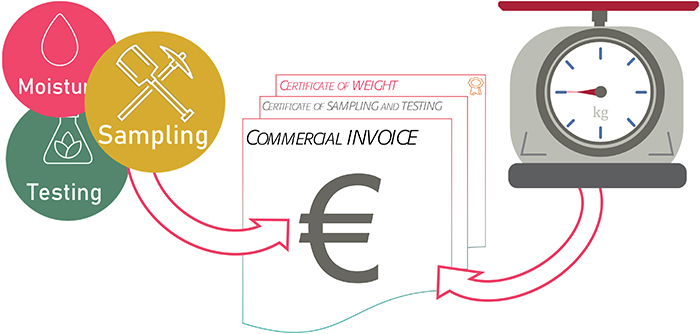
Figure 7. Sampling and weighing ultimately merge into one value: the one on the invoice.
References
- P. Gy, “Part IV: 50 years of sampling theory—a personal history”, Chemometr. Intell. Lab. Syst. 74, 49–60 (2004). https://doi.org/10.1016/j.chemolab.2004.05.014
- R.C.A. Minnitt and K.H. Esbensen, “Pierre Gy’s development of the Theory of Sampling: a retrospective summary with a didactic tutorial on quantitative sampling of one-dimensional lots”, TOS Forum Issue 7, 7–19 (2017). https://doi.org/10.1255/tosf.96
- R.C.A. Minnitt, “The Pierre Gy Oration”, TOS Forum Issue 8, 17 (2018). https://doi.org/10.1255/tosf.104
- K.H. Esbensen, “Pierre Gy (1924–2015): the key concept of sampling errors”, Spectrosc. Europe 30(4), 25–28 (2018). https://doi.org/10.1255/sew.2018.a1
- P. Gy, Sampling for Analytical Purposes. Wiley, Chichester (1998).
- K.H. Esbensen, Introduction to the Theory and Practice of Sampling. IMP Open, Chichester (2020). https://doi.org/10.1255/978-1-906715-29-8
- K.H. Esbensen, “TOS reflections: is there a third way? (to promote the Theory of Sampling)”, TOS Forum Issue 10, 21 (2020). https://doi.org/10.1255/tosf.122
- K.H. Esbensen, “Sampling commitment—and what it takes…”, Spectrosc. Europe 31(1), 24–28 (2019). https://doi.org/10.1255/sew.2019.a2
- K.H. Esbensen, “A tale of two laboratories I: the challenge”, Spectrosc. Europe 30(5), 23–28 (2018). https://doi.org/10.1255/sew.2018.a3
- K.H. Esbensen, “A tale of two laboratories II: resolution”, Spectrosc. Europe 30(6), 26–28 (2018). https://doi.org/10.1255/sew.2018.a4
- K.H. Esbensen and C. Wagner, “Why we need the Theory of Sampling”, The Analytical Scientist 21, 30–38 (2014).
- R.J. Romañach, A. Joubert Castro and K.H. Esbensen, “WHAT are sampling errors—and WHAT can we do about them? Part 1”, Spectrosc. Europe 33(2), 36–42 (2021). https://doi.org/10.1255/sew.2021.a11
- R.C.A. Minnitt, “Sampling: the impact on costs and decision making”, The Southern African Institute of Mining and Metallurgy 107, 460 (2007).
- D.A. Vogel, “Access, Select, Include – a review of the commercial sampling of traded bulk commodities in the context of Gy’s Theory of Sampling”, in Proceedings of the 8th World Conference on Sampling and Blending, Perth, Australia. The Australasian Institute of Mining and Metallurgy, Melbourne, pp. 367–378 (2018).

Aldwin Vogel
Duncan Aldwin Vogel (born in the Netherlands, 13 October 1973) is a global expert in weighing, sampling and testing of traded commodities. Already during his study in business management at the International School of Economics, Rotterdam, Aldwin started building his pedigree in the renowned family inspection business Hoff & Co. Services BV that became part of Bureau Veritas in 2010. From September 2011 to August 2013 Aldwin was based in Houston, USA, seconded as acting Director, Steel and Energy Products. Returning to Europe and the Metals & Minerals Trade Business Line in September 2013, Aldwin is now responsible for Technical Governance of Bureau Veritas’ Commodities Trade services globally. His expertise covers all aspects of inspection, sampling and analysis starting from green field prospect requirements to fully implemented turn-key projects. Embracing augmented inspection services through IoT and smart communication, Aldwin recently also came out as inventor and patent holder of several novel inspection solutions. He is highly experienced at all aspects of testing for Transportable Moisture Limit and was leader of the TML workgroup of the TIC Council. Aldwin is a delegate of the Netherlands on ISO Technical Committee 102 (Iron ore and direct reduced iron) and TC183 (Copper, lead, zinc and nickel ores and concentrates) where his focus is on sampling, sample preparation, moisture determination and TML. 0000-0003-0445-5259
0000-0003-0445-5259
[email protected]

Kim Esbensen
Kim H. Esbensen, PhD, Dr (hon), has been research professor in Geoscience Data Analysis and Sampling at GEUS, the National Geological Surveys of Denmark and Greenland (2010–2015), chemometrics & sampling professor at Aalborg University, Denmark (2001–2015), professor (Process Analytical Technologies) at Telemark Institute of Technology, Norway (1990–2000 and 2010–2015) and professeur associé, Université du Québec à Chicoutimi (2013–2016). From 2015 he phased out a more than 30-year academic career for a new quest as an independent researcher and consultant. But as he could not terminate his love for teaching, he is still very active as an international visiting, guest and affiliate professor. A geologist/geochemist/metallurgist/data analyst of training, he has been working 20+ years in the forefront of chemometrics, but since 2000 has devoted most of his scientific R&D to the theme of representative sampling of heterogeneous materials, processes and systems: Theory of Sampling (TOS), PAT (Process Analytical Technology) and chemometrics. He is a member of several scientific societies and has published over 250 peer-reviewed papers and is the author of a widely used textbook in Multivariate Data Analysis (35,000 copies), which was published in its 6th edition in 2018. He was chairman of the taskforce behind the world’s first horizontal (matrix-independent) sampling standard DS 3077 (2013). He is editor of the science magazine TOS forum and this Sampling Column. In 2020 he published the textbook: Introduction to the Theory and Practice of Sampling (impopen.com/sampling). 0000-0001-6622-5024
0000-0001-6622-5024
[email protected]

