Kim H. Esbensen
KHE Consulting (http://www.kheconsult.com) and Guest Professor (Denmark, Norway, Puerto Rico)
DOI: https://doi.org/10.1255/sew.2018.a1
© 2018 Spectroscopy Europe
The founder of the Theory of Sampling (TOS), Pierre Gy (1924–2015) single-handedly developed the TOS from 1950 to 1975 and spent the following 25 years applying it in key industrial sectors (mining, minerals, cement and metals processing). In the course of his career he wrote nine books and gave more than 250 international speeches on all subjects of sampling, including the all-persuasive aspect of hidden economic losses due to neglect of salient sampling issues. In addition to developing TOS, he also carried out a significant amount of practical R&D. But he never worked at a university; he was an independent researcher and a consultant for nearly his entire career—a remarkable scientific life. Gy himself wrote a five-paper personal scientific history published in 2004.1 We will dedicate a full Sampling Column to honour this remarkable man and his lifetime achievements later in this series. Should the reader be tempted to delve into this already now, however, a special issue of TOS Forum is available.2

Figure 1. Pierre Gy (1924–2015), founder of the Theory of Sampling (TOS), at one of his last public appearances (Porsgrunn, Norway, 2005). Photo credit: Kim H. Esbensen.
Rational understanding of heterogeneity and appropriate sampling
Gy’s breakthrough was to take on the overwhelmingly complex phenomenon of heterogeneity. The traditional route, taken by all his contemporaries (and usually based on very dubious assumptions), was to simplify. In his quest to be rational and complete, however, Gy identified no less than eight sampling errors that represent everything that can go wrong in sampling, sub-sampling (sample mass reduction), sample preparation and sample presentation—due to heterogeneity and/or inferior sampling equipment design and performance. Over a period of 25 years he meticulously worked out how to avoid committing such errors in the design, manufacture, maintenance and operation of sampling equipment and elucidated how their adverse impact on the total accumulated uncertainty could be reduced as much as possible when sampling in practice. It was a monumental job. Along the way, he studied for and was awarded two PhDs (in mineral processing and statistics) in order to be adequately equipped to solve the highly complex theoretical and practical problems identified. It is fair to say historically that Pierre Gy was the only scientist to tackle the full set of issues related to sampling of heterogeneous materials and processes.
As an illustration, consider the few examples of different materials shown in Figure 2 and try to imagine what mathematical approach would be appropriate in order to describe their heterogeneity?
Statistics—would very likely be the answer… But what kind, and level, of statistics? Pondering this issue, virtually everyone would likely want to get help via one, or more, type of “statistical distributions”. After all, we are dealing with heterogeneous materials. Analytical results stemming from repeated sampling will then not be similar, far less identical, but would have to follow a distribution of a kind. It may be more-or-less easy to find the right distribution (of analytical results), or it may be difficult. Also, is there one universal distribution ruling over all the world’s very different materials and their very different manifestations? This is definitely where one would like to enlist the experts, the statisticians. Surely this community will know which distribution would be appropriate, and/or will possess the knowledge and competence to find it.
Moving along, however, one would soon find oneself burdened by the necessity to state, to the statisticians, exactly what constitute the physical basis for all analytical results. And this would be where the headaches and severe sweating would start: the physical basis of all analytical result is the analytical aliquot (in the form of a small vial, for example). This view is tantamount to picturing the whole lot as a collection of very many, very small samples, aliquots. However, nobody in their right mind would try to sample a full lot by increments of the size of the final aliquot. On the other hand, from the approach delineated in these columns, it is clear that any aliquot is the result of a complex, multi-stage sampling, sub-sampling process. And this is the cardinal knowledge delineated: it is possible, indeed likely, that sampling processes can be carried out in ever so many and different ways, most of which are demonstrably non-representative. This would mean that it actually matters which specific sampling process was used to produce the final aliquot. Does this then mean that there are always many equally possible differing analytical results? Actually yes, if one is not acquainted with TOS and its distinction between representative sampling process, and worthless “specimenting”. Before sinking fully into this quicksand, the last thought will be… the aliquot must be representative of the whole lot: but how to get this imperative demand into the statistics?

Figure 2. The manifestations of heterogeneous materials are infinite. What would be the common approach to describing such different types of irregular “distributions”? And many intrinsic heterogeneity features are not visible to the naked eye, e.g., as illustrated by the truckload of grain shown bottom left. Pierre Gy undertook a 25-year long journey before he reached the destination: the Theory of Sampling (TOS). Photo credit: KHE Consulting (archives) and iStockphoto
Well, the answer to this is much more complex than might be suggested by a first reflection. First of all, the statisticians do not know the world’s very different materials and their very different heterogeneities; why should they? It is you, the sampler, who is the expert here. After some more reflection based on your own experiences, it will become clear that whereas statistics is addressing a population of ”units”, each of which are identical except for the differing analytical results, the “units” of a heterogeneous lot are defined by the specific nature of the material and the specific sampling procedure used, in particular by the increment, or sample, size (mass). Thus, in a very real sense, the final analytical results do indeed depend on the sampling procedure—a different sampling approach, e.g. grab sampling vs composite sampling, will assuredly give rise to different analytical results (with the composite sampling result being overwhelmingly more reliable… see all previous Sampling Columns). Go tell this to the statisticians… A direct inroad to this complexity, without all the math, can be found in Reference 3.
At the outset, then, we are not in a position to simply take over conventional statistical notions, populations, units. We are left to fend for ourselves: and this was exactly what Pierre Gy realised. Upon which he set himself the goal of developing the “appropriate statistics” with which to be able to describe the real-world of heterogeneous materials (and processes, see later) which is infinitely more complex than a world conceptualised as conventional vectors, matrices and arrays of data, which lend themselves to simple descriptions by statistical moments: averages, standard deviations, variances etc. For the interested reader, there are several, carefully crafted next-level introductions to this journey.4–7

Figure 3. There is no end to the many ways heterogeneity appears. Here a pronounced grain size segregation sometimes expresses itself dramatically (left), at other times completely “embedded” (top-right). It takes a radically different approach to be able to include such features in standard statistical distribution models, in fact Pierre Gy had to invent a new kind of “unit” in order to accomplish this goal, the “heterogeneity contribution”. Photo credit: KHE Consulting (archives).
There is hope, however
Although complex, TOS can in fact be made easily accessible. There are many systematic elements of the TOS, which makes mastering it possible, also from a decidedly less in-depth theoretical and mathematical level.
For example, the eight sampling errors originate from only three sources: the material (always heterogeneous, it is only a matter of degree), the sampling equipment (which can be designed either to promote a representative extraction, or not) and the sampling process (even correctly designed equipment can be used in a non-representative manner). In general, sampling is also defined by whether the lot is stationary or moving when sampling takes place, a distinction that is well-known within many application fields, in the realm of powders for example: “sample only when the powder is moving”.
And, the breakthrough: as it turned out, some sampling errors were found to be able to be eliminated completely, which simplifies the sampling agenda considerably. But it is, of course, necessary to know exactly how to identify these errors and exactly how to eliminate them. These are the so-called Incorrect Sampling Errors (ISE), a concept that was to be instrumental in order to be able to give a distinct definition of both a “correct” as well as a “representative” sampling process.
Following this rational simplification route, recently TOS has been presented in a fully axiomatic framework.8–10 Figure 4 shows the systematics of the complete framework of TOS’ General Principles (GP), Sampling Unit Operations (SUO) and all eight sampling errors, distinguished as ISE and Correct Sampling Errors (CSE). The value of this overview stems from the fact that all principal elements needed for a guarantee for a guaranteed representative pathway “from-lot-to-aliquot” are outlined here. This framework should be viewed as a master enabler for delving into the TOS literature in full.
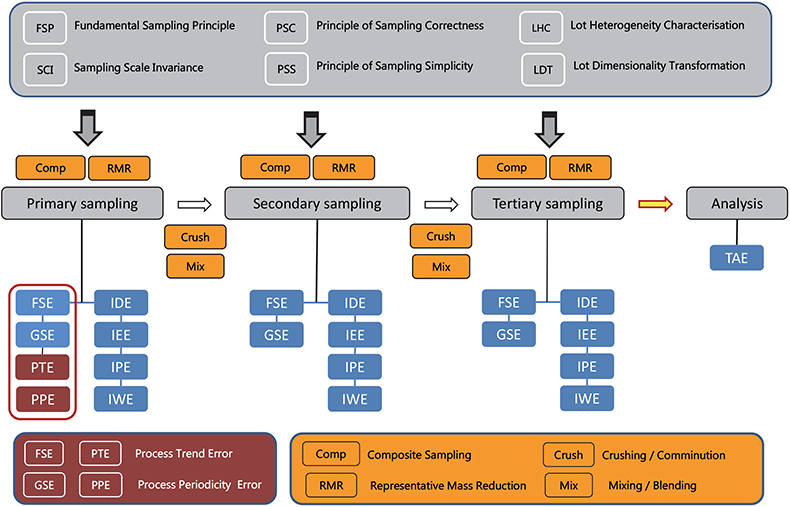
Figure 4. Theory of Sampling (TOS) synoptic overview, shown here for three sampling stages. TOS is comprised by six Governing Principles (GP) (top grey panel), four Sampling Unit Operations (bottom yellow panel) and eight sampling errors (blue/maroon). The basic differentiation between the ISEs (IDE, IEE, IPE, IWE) and the CSEs (FSE, GSE) will be covered in a future column. For details, see References 11–13 and other authoritative references therein. Illustration copyright KHE Consulting; reproduced with permission.
How to sample representatively: TOS
The first task on any sampling agenda is to eliminate the ISEs, mainly an issue regarding the design, installation, operation and maintenance of the sampling equipment. Subsequently, what remains, are the CSEs which can be dealt with by standard means, i.e. by increasing the number of composite sampling increments, Q, with respect to the empirical heterogeneity encountered (always honouring the Fundamental Sampling Principle, FSP) and always involving the pertinent GPs and other SUOs. Recent introductions to TOS, in general, are References 8, 9, 13, 14. In relation to the specific disciplines of chemometrics and multivariate data analysis in general, as well as in relation to pharmaceutical production, dedicated introductions can be found in References 5 and 15.
Figure 4 depicts a generic, multi-stage sampling process outline, the singular purpose of which is to deliver a representative analytical aliquot (yellow arrow). Sampling of stationary lots makes use of six basic sampling errors (blue), while process sampling (sampling of dynamic lots) needs two more errors to be tackled in full (maroon).
TOS logically demands that all pre-aliquot steps are supervised and governed by a unified sampling responsibility. This is a legal person, either in the form of a single individual (a “sampling czar”) or by a committee representing all departments in which sampling is performed. The latter situation is typical of very many organisational solutions in big companies and corporations; but is unfortunately also the reason behind a considerable proportion of the sampling problems met with in real life. Experience with many big corporations, companies and organisations unfortunately points to considerable difficulties expressly related to inter-departmental collaboration, or rather, to the lack thereof. Many are the cases where traditional rivalries between departments, individuals or just historical traditions make effective sampling across the entire “lot-to-analysis” pathway impossible. Even though such issues often are the main culprits behind what appear to be “impossible-to-solve” sampling problems, solutions rather come from the realm of organisational psychology. However, there also exist disruptive solution possibilities within the realm of TOS: it is most certainly not only the front-line sampler who need proper education with respect to TOS, because they collect the samples upon which analytical results are produced and upon which ultimately important decisions are made. Indeed, all individuals who are responsible for optimising sampling and process performance should feel a responsibility to become conversant with TOS. Thus, whether presidents, vice presidents, operations managers, process technicians, laboratory supervisors, quality assurance and quality control managers (see, for example, Reference 16) and indeed also concerned investors and company shareholders need a succinct understanding of TOS to be fully competent in their respective roles and capacities.
And it is all about how be able to identify and eliminate, or reduce, a small group of sampling errors—the legacy of Pierre Gy.
References
- P. Gy, “Sampling of discrete materials—a new introduction to the theory of sampling I. Qualitative approach”, Chemometr. Intell. Lab. Syst. 74, 7–24 (2004) doi: https://doi.org/10.1016/j.chemolab.2004.05.012; P. Gy, “Sampling of discrete materials II. Quantitative approach—sampling of zero-dimensional objects”, Chemometr. Intell. Lab. Syst. 74, 25–38 (2004) doi: https://doi.org/10.1016/j.chemolab.2004.05.015; P. Gy, “Sampling of discrete materials III. Quantitative approach—sampling of one-dimensional objects”, Chemometr. Intell. Lab. Syst. 74, 39–47 (2004) doi: https://doi.org/10.1016/j.chemolab.2004.05.011; P. Gy, “Part IV: 50 years of sampling theory—a personal history”, Chemometr. Intell. Lab. Syst. 74, 49–60 (2004) doi: https://doi.org/10.1016/j.chemolab.2004.05.014; P. Gy, “Part V: Annotated literature compilation of Pierre Gy”, Chemometr. Intell. Lab. Syst. 74, 61–70 (2004) doi: https://doi.org/10.1016/j.chemolab.2004.05.010
- “Pierre Gy (1924–2015)—in memoriam”, TOS Forum Issue 6 (2016). https://www.impopen.com/tosf-toc/16_6
- K.H. Esbensen, “Materials properties: heterogeneity and appropriate sampling modes”, J. AOAC Int. 98, 269–274 (2015). doi: https://doi.org/10.5740/jaoacint.14-234
- K.H. Esbensen, “Sampling – theory and practice”, Alchemist Issue 85, 3–6 (August 2017), London Buillion Market Association.
- K.H. Esbensen, R.J. Romanach and A.D. Roman-Ospino, “Theory of Sampling (TOS) – a necessary and sufficient guarantee for reliable multivariate data analysis in pharmaceutical manufacturing”, in Multivariate Analysis in Pharmaceutical Industry, Ed by A.P. Ferreira, J.C. Menezes and M. Tobin. Academic Press, Ch. 4 (2018). doi: https://doi.org/10.1016/B978-0-12-811065-2.00005-9
- K.H. Esbensen and P. Paasch-Mortensen, “Process sampling: Theory of Sampling – the missing link in Process Analytical Technology (PAT), in Process Analytical Technology, 2nd Edn, Ed by K.A. Bakeev. Wiley, Ch. 3 (2010). doi: https://doi.org/10.1002/9780470689592.ch3
- K.H. Esbensen, C. Paoletti and N. Theix, “Representative sampling for food and feed materials: a critical need for food/feed safety”, J. AOAC Int. 98(2), 249–251 doi: https://doi.org/10.5740/jaoacint.SGE_Esbensen_intro
- K.H. Esbensen and C. Wagner, “Why we need the Theory of Sampling”, The Analytical Scientist, Issue 21, 30–38 (2014).
- K.H. Esbensen and C. Wagner, “Theory of Sampling (TOS) versus measurement uncertainty (MU) – a call for integration”, Trends Anal. Chem. 57, 93–106 (2014).
- DS 3077. Representative Sampling—Horizontal Standard. Danish Standards (2013). www.ds.dk
- F.F. Pitard, Pierre Gy’s Sampling Theory and Sampling Practice: Heterogeneity, Sampling Correctness, and Statistical Process Control.CRC Press (1993). ISBN: 978-0-849-38917-7
- P. Gy, Sampling for Analytical Purposes, 1st Edn. Wiley, New York (1998). ISBN: 978-0-471-97956-2
- R.C.A. Minnitt and K.H. Esbensen, “Pierre Gy’s development of the Theory of Sampling: a retrospective summary with a didactic tutorial on quantitative sampling of one-dimensional lots”, TOS Forum Issue 7, 7–19 (2017). doi: https://doi.org/10.1255/tosf.96
- K.H. Esbensen and L.P. Julius, “Representative sampling, data quality, validation – a necessary trinity in chemometrics”, in Comprehensive Chemometrics, Ed by S. Brown, R. Tauler and R. Walczak. Elsevier, Oxford, Vol. 4, pp. 1–20 (2009). doi: https://doi.org/10.1016/B978-044452701-1.00088-0
- K.H. Esbensen and B. Swarbrick, Multivariate Date Analysis – An introduction to Multivariate Data Analysis, Process Analytical Technology and Quality by Design, 6th Edn. CAMO Software AS (2018). ISBN 978-82-691104-0-1
- K.H. Esbensen and C.A. Ramsey, “QC of sampling processes—a first overview: from field to test portion”, J. AOAC. Int. 98, 282–287 (2015). https://doi.org/10.5740/jaoacint.14-288

