Chuck Ramseya and Kim H. Esbensenb
aPresident EnviroStat, Inc., http://www.envirostat.org, [email protected]
bPresident KHE Consulting, Copenhagen, Denmark. https://kheconsult.com/, [email protected]
DOI: https://doi.org/10.1255/sew.2022.a6
© 2022 The Authors
Published under a Creative Commons BY-NC-ND licence
Sampling is nothing more than the practical application of statistics. If statistics were not available, then one would have to sample every portion of an entire population to determine one or more parameters of interest. There are many potential statistical tests that could be employed in sampling, but many statistical tests are useful only if certain assumptions about the population are valid. Prior to any sampling event, the operative Decision Unit (DU) must be established. The Decision Unit is the material object that an analytical result makes inference to. In many cases, there is more than one Decision Unit in a population. A lot is a collection (population) of individual Decision Units that will be treated as a whole (accepted or rejected), depending on the analytical results for individual Decision Units. The application of the Theory of Sampling (TOS) is critical for sampling the material within a Decision Unit. However, knowledge of the analytical concentration of interest within a Decision Unit may not provide information on unsampled Decision Units; especially for a hyper-heterogenous lot where a Decision Unit can be of a completely different characteristic than an adjacent Decision Unit. In cases where every Decision Unit cannot be sampled, application of non-parametric statistics can be used to make inference from sampled Decision Units to Decision Units that are not sampled. The combination of the TOS for sampling of individual Decision Units along with non-parametric statistics offers the best possible inference for situations where there are more Decision Units than can practically be sampled.
Introduction
There are heterogeneous materials and there are heterogeneous lots. Materials can be heterogeneous in the sense of dissimilarity between the fundamental constituent units of the material, e.g. particles (and fragments thereof), grains, minerals, cells biological units … (this is the definition of heterogeneity in the Theory of Sampling, TOS). Lots can be heterogeneous in the sense of dissimilarity between the characteristics of Decision Units (DU). Moreover, there are types of hyper-heterogeneous lots with significant internal complexity, which can be known or hidden. Below, lots of this latter type are in focus.
For many hyper-heterogeneous lots with complex internal structure(s), i.e. lots containing groups of more-or-less distinct DUs, complete sampling is, in practice, often impossible due to logistical, economical or other restrictions. Such lots cannot be sampled reliably on the basis of an assumed distribution, i.e. the distribution of the analyte(s) between the DUs does not follow any known distribution, making the archetype statistical inference based on a known distribution inadequate. Instead, the basis for the statistical inference of these types of lots is the non-parametric one-sided tolerance limit, which can be applied to all types of lots from uniform to hyper-heterogeneous, but which is especially relevant for the type of hyper-heterogeneous lots exemplified in this contribution.
This column shows the critical importance of the application of non-parametric statistical methods when there are more DUs present than can be sampled as an essential complement to the TOS. This situation in fact occurs in very many contexts, for very many sampling targets and materials and lots. What to do?
Different manifestations of heterogeneity
There is heterogeneity, and there is heterogeneity—there are heterogeneous materials within a DU and there is heterogeneity between DUs. Materials can be heterogeneous in the sense of the TOS reflecting dissimilarity between the constituent units of the material (particles and fragments thereof, grains, cells, other …) within a DU. Readers may be familiar with this type of sampling, see Reference 1 and further key references therein. There is a special focus on heterogeneity in this TOS sense in Reference 2.
Multiple DUs can be heterogeneous in the sense of differences between the characteristics of DUs, which can be defined more-or-less appropriately. An introduction to sampling of lots of this type is found in Reference 3.
Moreover, there are types of heterogeneous lots with even more internal complexity, which may be known or may be hidden. This column presents a rationale for how to sample such hyper-heterogeneous lots, or more precisely how to sample in the presence of heterogeneity both within and between DUs.
A hyper-heterogeneous lot with hidden structure
An illustrative example of a hyper-heterogeneous lot shall be a legacy nuclear waste mega-lot (see Acknowledgements). Over a period of 50 years, extensive decommissioning of nuclear facilities and several temporary low-level nuclear waste storage facilities have been established, Figure 1, from which waste drums can be retrieved on demand in principle, but in practice associated with various degrees of logistical constraints. In total, there are today ~66,000 conditioned waste drums in temporary storage depots.
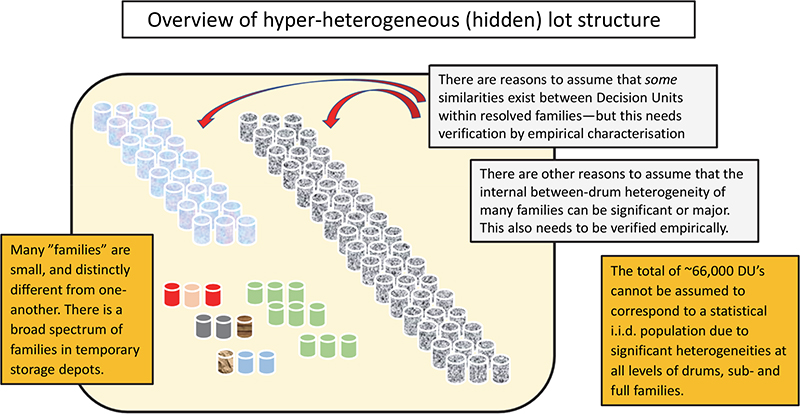
Figure 1. Illustration of a hyper-heterogeneous lot comprised by a hierarchy of units: drums – families – lot. For the discussions that follow, the operationally relevant DU is an individual drum.
In 2021–2023 the time has come to start engaging in final end-storage of this legacy nuclear waste. Today there are much stricter Waste Acceptance Criteria (WAC) in play than was the case in earlier decades, for which reason there is a critical need to pre-check “all” drums with the aim of reaching an operative classification into three categories: 1) Cleared for “Final storage”; 2) “Re-classification to intermediate/high-level storage”; or 3) “Needs further treatment”. The sampling methodology needed for physical, chemical and radiological inspection of selected individual drums has been described by Tuerlinckx and Esbensen.4
The current Herculean task is how to inspect ~66,000 drums for a) physical characteristics; b) chemical characteristics; and c) radioactivity characteristics, which make use of very different types of analytes. With current economic budgets vs the prevailing practical conditions, complete inspection of all ~66,000 drums is likely not feasible, however desirable. In addition, the consequences of an incorrect decision are very serious.
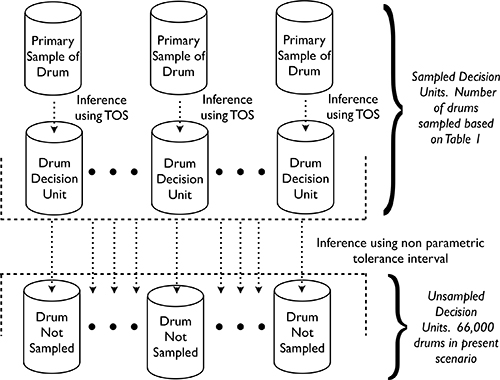
Figure 2. Illustration of inference from multiple sampled to unsampled DUs.
It would have been nice if the ~66,000 drumsa could be viewed as one statistical population consisting of i.i.d. DUs with a known distribution between DUs. But because of the 50-year complex decommissioning history it is known that low-level nuclear waste drums not only differ extremely in compositional content(s), physical constitution and radioactivity profiles, but—horror-of-horrors from a statistical point of view—there are very good reasons to infer that there exist groupings within this population of 66,000 DUs. But the degree to which such groupings (“families” in the nuclear expert lingo) are well characterised and well discriminable inter alia, is markedly uncertain; some families are suspected to be clearly demarked, but certainly not all, or maybe not even most.
aIn the nuclear waste realm, often waste drums may even have their own internal heterogeneity, i.e. containing 1, 2 or 3 compressed units (called “pucks”), which may then better reflect the optimal resolved DUs of interest, depending on the specific WAC analytes proscribed. For simplicity in this didactic exposé of statistical methodology however, we here stay with DUs being synonymous with drums.
So far, diligent archival work has resulted in identification of some 40+ “families” or so, each with broadly similar radioactivity profiles. It is relatively easy to measure a radioactive profile fingerprint of an individual drum.4 Due to the marked heterogeneity hierarchy (drums – families – meta-population), Figure 1, it was at one time tentatively decided to try to use “resolved families” as DUs, rather than the entire lot, as laid out by Ramsey.3 The main statistical issue then was whether it was possible to estimate how many drums would be needed to characterise (or validate) each family with a desired low “statistical uncertainty”. Further comprehensive problem analysis, however, made it clear it was necessary to increase the observation resolution to focus on individual drums as the final operative DUs.
Statistical methodology
The basis for the statistical sampling which must be used for this type of nebulous lot is the non-parametric one-sided tolerance limit, a test that does not depend on any distribution of measurement results. The statistical theory behind this test is described in many statistical textbooks.5–7
Operative statistical approach
Here follows a generic sampling plan that can be applied to hyper-heterogeneous lots in general:
- Appropriate definition of DUs—in the present scenario, an individual waste drum.
- Determine the Data Quality Objectives for the project: Project management must decide its wish for a confidence level (X %) that no more than Y % of the drums may fail the chemical WAC. The confidence level and Y % shall be determined a priori, without any consideration of, or influence from, the statistically required number of samples (see further below). If project management decides to decree 100 % confidence that 0 % fail WAC criteria (a common request), then there is unfortunately nothing that can be done. Then there must be 100 % inspection of all DUs and there must be zero sampling and analytical error—this is obviously an impossibility.
- Statistical criterion: Statistical sampling includes the possibility that some failing DUs may be missed. This potential is to be balanced by the tremendous reduction in sampling and analytical costs achievable by carrying out statistical sampling of only a fraction of the total population of DUs. To determine the sampling effort required, the X confidence and Y percent must be determined prior to calculating the required number of drums to be physically sampled. It is the responsibility of project management to decide on its wish independently and a priori of working out the sampling plan. Most importantly, do not first select the required number of samples to be extracted, for example based on project economics, logistics or some other bracketing factor, and then accept what the confidence level and risk percent based on this number turns out to be. The confidence level and risk percent must only be based on considerations of the consequences of an incorrect statistical decision (Table 1).
Statistical clarification: The percent of drums that may fail does not imply that any of the unsampled drums will fail, just that many could possibly fail and that this would be detectable. The number of samples required for any combination of confidence and proportion of DUs can be determined from the master equation shown in the Appendix illustration, based on Reference 6.
Table 1. Statistically required number of samples to be extracted from a population.a,b In this table, “failing” means a maximum amount that could fail, not implying that any will fail.
Confidence level (X): 90 % | |||
Y % DUs failing | 10 % | 5 % | 1 % |
Number samples | [22] | [45] | [230] |
Confidence level (X): 95 % | |||
Y % DUs failing | 10 % | 5 % | 1 % |
Number samples | [29] | [59] | [299] |
Confidence level (X): 99 % | |||
Y % DUs failing | 10 % | 5 % | 1 % |
Number samples | [44] | [90] | [459] |
aThe required number of samples can be calculated for any combination of confidence level and percent.
bIf the number of drums required to be sampled approaches the total number (greater that 10 %) in a population (or in a resolved family or another sub-set of the complex lot), the required number of samples can be reduced by application of the so-called finite population correction. In this case seek further statistical assistance.
- Action plan: Select and retrieve required number of drums at random from the total population of drums. It is imperative that any drum selected in the statistical sampling plan is fully available for sampling and can be extracted without any undue restrictions in practice.
Statistical conclusion: If none of the extracted drums fail the chemistry WAC, project management can be “X % confident that no more than Y % of the drums fail the chemical WAC”. Since these Data Quality Objectives have been decided a priori, this means that the project can dispose of all drums in the population without further verification regarding the operative WAC. It is noted that this statistical test assumes that there is no sampling error and no analytical error. While this cannot ever be the case, in practice it is imperative that these errors be controlled as much as possible to provide reliable conclusions, see Reference 8.
However—and this is the whopper of all inferential statistics: - If one or more of the DUs fail the chemical WAC criteria, the Data Quality Objectives have not been met, and additional sampling and analysis of drums must be performed.
In this case there are several options to continue the characterisation project. It is imperative to develop such alternatives in collaboration with all stakeholders and parties involved, frontline scientific and technical personal, project management, overseeing boards a.o.
One possible course of action could be to compare the sampled drums with their radiological profiles to see if there is a correlation between the radiological profile and the chemical parameters in the WAC. There could then, perhaps, be established a multivariate data model, aka a chemometric model.9 If this is the case, it may perhaps be possible to classify all the drums in the population into operative sub-populations (a la the presently resolved ~40 radiological families) as a basis for repeating steps 1–3 above, specifically now addressing the array of resolved sub-populations (“families”) individually. This approach could be attempted for any relevant WAC (radiological, chemical, physical, other …). N.B. This model must be validated on additional random DUs, since it is easy to constrain a model to fit the available data. The critical issue is to test the model, to validate the model on a new set of randomly selected DUs (“test set validation”). The number of samples to verify any model will be that same as initially determined since the data quality objectives do not change. It makes no sense to try out just a moderate number of additional samples. The power of non-parametric statistics lies in the number of DUs with which to cope with hyper-heterogeneous lots; this is a hard problem.
Take home lesson
The objective of this issue’s contribution is to present a type of lot heterogeneity for which all types of parametric statistics is not applicable (based on assumed, or proven, normal distribution, nor any other parametric distribution). While the above approach is illustrated by a lot with rather specific features, it well illustrates the general characteristic for which non-parametric statistical inference can deal with complex, partially or wholly, hidden structure(s).
Table 1 shows the evergreen question raised when seeking help from statistics: “how many” observations or measurements are needed in this generic non-parametric approach, presented for a few typical cases i.e. (90, 95, 99 %) confidence that no more than (10, 5, 1 %) DUs could be failing. The smallest vs the largest necessary number of samples needed to allow this test regimen could be from just a few to thousands, depending on the Data Quality Objectives. The power of generalisation is awesome, since this test scenario is applicable to all kinds of lots (populations) where it is not possible to sample all DUs—that’s quite a broad swath of the material world in which sampling is necessary!
A prominent “someone” from the sampling community, not a professional statistician, when presented with this non-parametric approach for the first time, exclaimed: “But these are magic numbers—they apply to everything, to every lot with such ill-defined characteristics. This is fantastic! Where do these numbers come from?”
The science fiction author Isaac Asimov (Figure 3) once pronounced: “Any sufficiently developed technology, when assessed on the basis of contemporary knowledge, will be indistinguishable from magic”.

Figure 3. Isaac Asimov: he knew a thing or two about science and technology, and the human condition. Credit: Jim DeLillo/Alamy Stock Photo
A perspective from the point of view of confidence vs reliability
John Young (1930–2018), by many considered the consummate astronaut, was a.o. the only astronaut to fly both in NASA’s Gemini, Apollo and Space Shuttle programmes; he flew in space six times in all. For an absolutely fascinating life’s story, see Reference 10; or his entry in Wikipedia.
After a “stellar” career as an active astronaut, in 1987 he took up a newly created post at the Johnson Space Center as Special Assistant for Engineering, Operations and Safety. In this position Young became known, rightly so, as the memo guy, producing literally hundreds of memos on all matters related to crew safety, most definitely not afraid to ruffle more than a few feathers when he felt the need. Safety was foremost in his mind. Young knew better than anyone that space flight is a very risky business, but he also knew the importance of paying attention to detail—and always doing things right.

Figure 4. October 1971 portrait photograph of John W. Young. Credit: NASA
From this plethora of safety missives, here is a small nugget—a gem rather in the present context (Reference 10, pp. 314–315):
“Sometimes the absurdity of bureaucratic logic was tough to take. Consider the case of the solid rocket motor (SRM) igniter. At the flight readiness review for STS-87 (….), we heard a report saying that the solid rocket motor igniter had undergone twelve changes. The changes, along with some other involving the manufacturer, has occasioned the test-firing of six new igniters. Something called “Larson’s Binomial Distribution Nomograph on Reliability and Confidence Levels” indicated that firing six igniters with zero failures gave us 89 % reliability with 50 % confidence. To raise that to 95 % reliability with 50 % confidence would take fourteen firings, while raising it to 95 % reliability with 90 % confidence would take forty-three firings. So, stupid me, I asked that we continue firing igniters to upgrade our confidence. Clearly it was far cheaper, I thought, to gain confidence than to experience a failure of the SRM igniter in what was only a flight test.”
Not related to the present column, but interesting, and funny, is Young’s next paragraph:
“So, what was the response to my suggestion? I was told that the plant that manufactured the igniters had been moved. Later, I was told that the manufacturing plant had not been moved and, ‘therefore’, firing six igniters should be enough. ‘Therefore?’”
Epilogue: carrying over
So, no magic—just the right kind of inferential statistics to the rescue for this type of “difficult to sample” lot or population.
However, an immediate apropos, which is non-negotiable: all physical sampling of the individual DUs selected and extracted, must be compliant with the stipulations, rules and demands for representative sampling laid down by the TOS. This is an essential approach when the destructive testing is required, no exceptions.
There are many other types of lots with similar characteristics as the ones selected for illustration here to be found across a very broad swath of sectors in science, technology, industry, trade and environmental monitoring and control. For example, from the food and feed sector, from which can be found key examples in Reference 11. Or from the mining realm: primary sampling of broken ore accumulations12,13 as brought to the mill in haphazardly collected truck loads, while sampling for environmental monitoring and control is a field in which the present approach finds extensive applications. It is instructive to acknowledge that the within-DU as well as the between-DU heterogeneity characteristics from such dissimilar application fields, food vs ore are identical, it is just a matter of degree.2
Appendix
Where and how to find appropriate “magic numbers”
The Larson nomogram (Figure 5) can be used to obtain the required sample numbers presented in this paper. This nomogram was developed in 1966, long before the proliferation of computers, and is based on the binomial distribution. To use the nomogram, draw a line from the desired “confidence” to the “percent” one is willing to allow to fail. The intersection of that line to the line of “n Sample size” gives the necessary number of samples to inspect. With this methodology, an exact determination is impossible, but readings from the nomogram are consistent with calculated values.
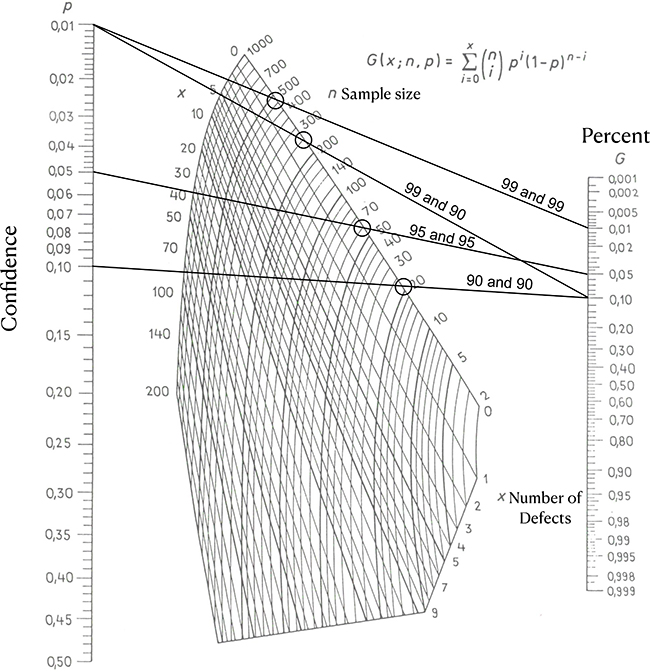
Figure 5. The Larson nomogram. Four circles indicate the required number of samples, found where lines connecting the desired “Confidence” with the desired “Percent” intersect the edge labelled “n Sample size”. Also note bottom part where this edge is labelled “x Number of Defects” (see text). Wikimedia Commons.
Larson developed this nomogram for lot acceptance sampling. Lot acceptance sampling is where and entire lot of individual DUs is accepted or rejected, depending on the acceptable failure rate of individual DUs within the lot. This is very common in statistical quality control. In traditional acceptance sampling any failure rate can be established.
In the scenario presented in this paper, the desired failure rate is zero, but that cannot be achieved without 100 % inspection. Therefore, there needs to be balance between the economics of 100 % inspection and the possibility that (a) drum(s) may be mischaracterised.
The Larson nomogram also provides values allowing for some defects—notice that many more samples are required in that case. While it is statistically equivalent, this approach (allowing a few defects) is not applicable for the scenario used in this paper since we here show the case in which we are not willing to knowingly allow any failing DUs. But this possibility offers an interesting view into even more broad applications, see, for example, References 3, 5, 14–17.
Acknowledgements
The authors acknowledge inspiration to use the generic nuclear waste scenario concept from work with BELGOPROCESS, greatly appreciated. It is clear, however, that the approach described above in this specific context is of much wider general usage ….
References
- K.H. Esbensen, Introduction to the Theory and Practice of Sampling. IM Publications Open (2020). https://doi.org/10.1255/978-1-906715-29-8
- K.H. Esbensen, “Materials properties: heterogeneity and appropriate sampling modes”, J. AOAC Int. 98, 269–274 (2015). https://doi.org/10.5740/jaoacint.14-234
- C.A. Ramsey, “Considerations for inference to decision units”, J. AOAC Int. 98(2), 288–294 (2015). https://doi.org/10.5740/jaoacint.14-292
- R. Tuerlinckx and K.H. Esbensen, “Radiological characterisation of nuclear waste—the role of representative sampling”, Spectrosc. Europe 33(8), 33–38 (2022). https://doi.org/10.1255/sew.2021.a56
- R.E. Walpole, R.H. Myers, S.L. Myers and K. Ye, Probability and Statistics for Scientists and Engineers, 9th Edn. Prentice Hall (2011).
- G.J. Hahn and W.K. Meeker, Statistical Intervals. John Wiley & Sons (1991). https://doi.org/10.1002/9780470316771
- D.R. Helsel, Nondetects and Data Analysis, Statistics for Censored Environmental Data. John Wiley & Sons (2005).
- C. Ramsey, “The effect of sampling error on acceptance sampling for food safety”, Proceedings of the 9th World Conference on Sampling and Blending, Beijing (2019).
- K.H. Esbensen and B. Swarbrick, Multivariate Data Analysis: An Introduction to Multivariate Analysis, Process Analytical Technology and Quality by Design, 6th Edn. CAMO Publishing (2018). ISBN 978-82-691104-0-1
- J. Young (with James R. Hansen), Forever Young: A Life in Adventure in Air and Space. University Press of Florida (2012). ISBN 978-0-8130-4933-5
- K.H. Esbensen, C. Paoletti and N. Theix, (Eds), “Special Guest Editor Section (SGE): sampling for food and feed materials”, J. AOAC Int. 98(2), 249–320 (2015).
- S.C. Dominy, S. Purevgerel and K.H. Esbensen, “Quality and sampling error quantification for gold mineral resource estimation”, Spectrosc. Europe 32(6), 21–27 (2020). https://doi.org/10.1255/sew.2020.a2
- S.C. Dominy, H.J. Glass, L. O’Connor, C.K. Lam, S. Purevgerel and R.C.A. Minnitt, “Integrating the Theory of Sampling into underground mine grade control strategies”, Minerals 8(6), 232 (2018). https://doi.org/10.3390/min8060232
- D. Wait, C. Ramsey and J. Maney, “The measurement process”, in Introduction to Environmental Forensics, 3rd Edn. Academic Press, pp. 65–97 (2015). https://doi.org/10.1016/B978-0-12-404696-2.00004-7
- C.A. Ramsey and C. Wagner, “Sample quality criteria”, J. AOAC Int. 98(2), 265–268 (2015). https://doi.org/10.5740/jaoacint.14-247
- C.A. Ramsey and A.D. Hewitt, “A methodology for assessing sample representativeness”, Environ. Forensics 6(1), 71–75 (2005). https://doi.org/10.1080/ 15275920590913877
- C.A. Ramsey, “Considerations for sampling contaminants in agricultural soils”, J. AOAC Int. 98(2), 309–315 (2015). https://doi.org/10.5740/jaoacint.14-268

Chuck Ramsey
Chuck Ramsey’s experience includes seven years with the National Enforcement Investigations Center (NEIC) of USEPA. While with the EPA, Mr Ramsey provided sampling and statistical expertise on all major regulations including Department of Justice, FBI, State Attorney Generals, regional EPA offices, state environmental departments and to industry through professional organisations. Mr Ramsey is involved with the development and review of regulations and guidance documents for sampling and statistics. He is a recognised expert in the areas of statistics and sampling and has served as an expert witness in several enforcement cases. He has given numerous presentations and courses on sampling, statistics and related topics at conferences and workshops. Mr Ramsey has conducted numerous consulting projects in the nuclear energy sector and for the US military, most of which are governed by non-disclosure agreements. Mr Ramsey is currently involved as a consultant in project BESTE (BELGOPROCESS).
[email protected]

Kim Esbensen
Kim H. Esbensen is an international expert and consultant in sampling (Theory of Sampling, TOS), chemometrics and PAT (Process Analytical Technology). Through a 35-year academic career involving three professorships, he has conducted R&D across a wide range of application fields, primarily in process industries (mining, minerals extraction and processing, bio-fuels, recycling, environmental monitoring, nuclear waste) in environmental science a.o. In 2015 he established an international consultancy (KHE Consulting). Esbensen has been responsible for a university educational programme straddling 30+ years in chemometrics, PAT, TOS, instrumental analysis, Multivariate Image Analysis (MIA), process technology and Philosophy of Science, currently in the form of a continuing education curriculum offered via KHE Consulting. His CV lists ~300 publications and ~400 lectures/presentations. He is a recipient of the Pierre Gy Sampling Gold Medal (2013), and the Russian Chemometrics Society Gold Medal (2012). In 2003 he inaugurated the biannual series of World Conferences on Sampling and Blending (WCSB), now in its 10th edition—https://wcsb10.com. Esbensen is editor of the scientific magazine TOS Forum and of the Sampling Column in Spectroscopy Europe/World. Esbensen’s credentials are documented in full at KHEC’s website: https://kheconsult.com. Mr Esbensen is currently involved as a consultant in projects BESTE and NOIR (BELGOPROCESS). 0000-0001-6622-5024
0000-0001-6622-5024
[email protected]

