Karin Engströma and Kim H. Esbensenb
aPhD Student & Method development engineer in sampling and analytical test methods
bKHE Consulting (www.kheconsult.com) & Guest professor (Denmark, Norway, Puerto Rico)
Karin Engström, LKAB mining, Kiruna, Sweden, continues to present illuminative cases from process industry. Here she reveals more from her ongoing PhD project showing application of variographic characterisation for on-line continuous control of process sampling systems, including the one that was validated according to current ISO standards guidelines in the previous column (monitoring a particular iron ore pellet stream). Together, the cases presented constitute a broad didactic showcase of the power of variographic analysis and problem-specific interpretations.
Variographic analysis
Variographic process data analysis was presented in a previous column, and the elements of TOS it is based upon have been introduced across the complete column series. For more theoretical background regarding the theory and practical application of the variogram see, for example, References 1–4. This column exclusively addresses application in the industrial domain, particularly regarding the possibility to conduct continuous on-line measurement system control. The key issue is that the total measurement system variability is composed by both the Total Sampling Error (TSE) plus the Total Analytical Error (TAE) contributions.
Continuous control of sampling systems
Validation of newly installed, recently upgraded or modified industrial sampling systems is essential for reliable process monitoring. This ensures documentation of representative samples and correct analytical results. Validation of sampling systems has traditionally been based on carefully extracted physical samples or by the use of calibrated PAT sensor technologies.
However, continuous control of existing sampling systems is equally important to ascertain that representativity is not infringed upon due to undetected changes in the sampling or process systems (trends, periodicity, equipment drift, upsets or component replacement etc.). Furthermore, this can ensure that the measurement system still functions satisfactorily if/when significant material compositional changes are introduced. Continuous variographic characterisation is a powerful tool for inspecting the sum of all the components that are contributing to the observable process variability over time. Variographic analysis can identify and quantify, as well as distinguish between sampling , analysis and process variabilities Variographic analysis can decompose the total apparent process variability. This method can, therefore, be used to detect changes in any source of variability, no matter if it originates from the process or from the sampling system.
This column presents a selected set of examples where variographic analysis has been applied to operating sampling systems at LKAB concentrating and pelletising plants, serving as examples of the information that can be derived through the use of variographic analysis.
9–12.5 mm size fraction of iron ore pellets
Size analysis of iron ore pellets is performed by the sampling system validated in the previous column, a linear cross stream sampler collecting primary samples every five minutes. The complete sampling system is automated with subsequent rotary mass reduction sub-sampling and automatic size analysis, presenting results approximately every hour. The variogram and process data for the 9–12.5 mm size fraction is presented in Figure 1. Successive variograms present similar results over several time periods, indicating similar sampling and analytical variability as was observed during the validation experiment.
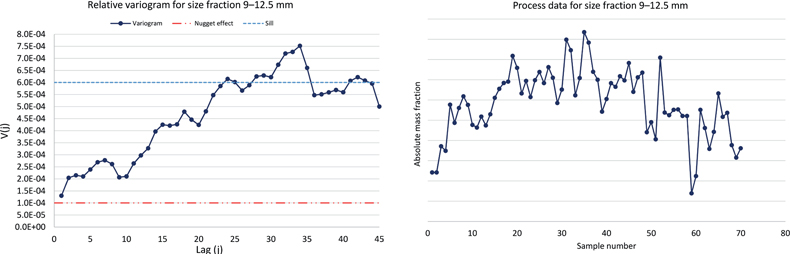
Figure 1. Variogram and process data for the 9–12.5 mm size fraction of iron ore pellets. Sill, blue line; nugget effect, red line. The nugget effect to sill ratio equals to approximately 15%.
Variograms must always be presented together with the raw process data from which they are derived. The interpretation of the size fraction variogram is particularly easy and clear in this case. As would be expected from general TOS experiences, a well-calibrated and maintained linear cross stream sampling system should give a reliable picture of the true process variation. This can be seen by the fact that the nugget effect to sill ratio is only approximately 15%, indicating that the total sampling and analytical variability does let through a highly satisfactory depiction of the process variation. The on-line sampling system is validated and can be continuously verified as fit-for-purpose representative.
Specific surface area of magnetite slurry
The specific surface area (SSA) of magnetite slurry is an important parameter for the process of balling iron ore pellets. The surface area is determined in the milling of the ore and is used for backward process control of the same milling process. The sampling system for SSA is a continuous primary sampling using a shark fin sampler in concentrating plant 3 and spear collection of a continuous flow from a pressurised pipe in concentrating plant 2. Both these sampling systems violate TOS’ Fundamental Sampling Principle (FSP) by not acquiring a complete cross-section of the slurry stream, but only collecting a part of the stream all of the time. Whether this impairs proper process control in practise is, amongst other things, related to the degree of heterogeneity of the flowing material; well-mixed material might be sampled fit-for-purpose, while significantly heterogeneous material will fare differently!
The secondary sampling for SSA in plant 3 consists of a grab sample collected from the primary sample stream every four hours, much maligned by TOS. However, the secondary sampling for SSA in plant 2 is a TOS-correct increment sampling, collecting and combining several increments to a composite sample accessed for analysis every four hours. The samples from both plants are analysed according to the Blaine method using an automatic analyser.
The variograms for SSA sampling systems in plant 2 and 3 show similar nugget effects (absolute magnitudes) in all produced variograms. However, the sill levels change significantly over different time periods analysed. Three example variograms are presented in Figures 2 and 3.
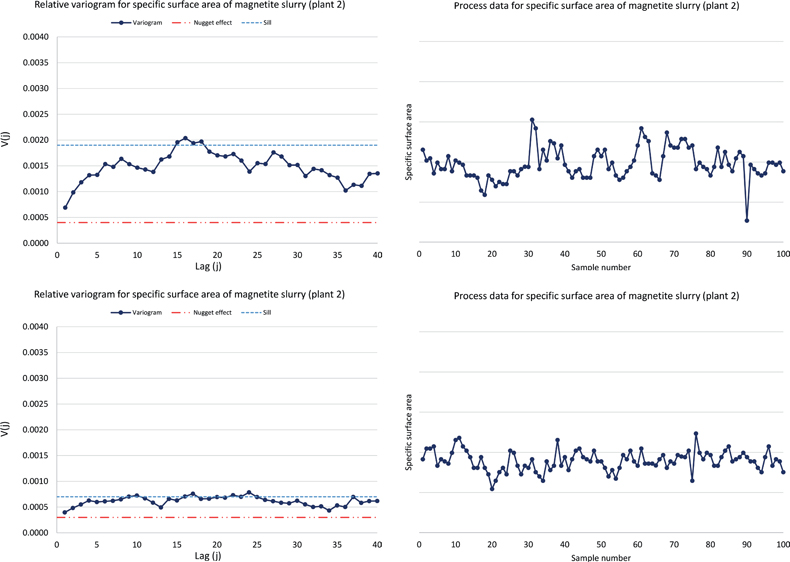
Figure 2. Variograms and process data for the SSA sampling system in plant 2 (TOS-correct secondary sampling). The two variograms are from different time periods, showing similar nugget effects but significantly different sill levels (see text). Sill, blue line; nugget effect, red line.
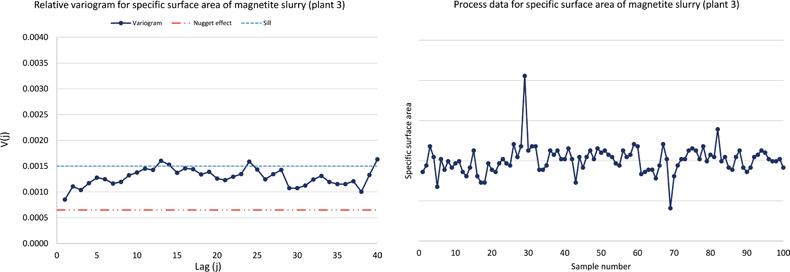
Figure 3. Variograms and process data for the SSA sampling system in plant 3 (secondary grab sampling, TOS-incorrect). Sill, blue line; nugget effect, red line. The variogram show similar nugget effect as plant 2.
The first variogram for plant 2 reveals a satisfactory performance for the total measurement system, with a nugget effect to sill ratio of approximately 20%, allowing a fair picture of the true process variations. In the second variogram for plant 2, the nugget to sill ratio is approximately 50%, which could lead to the conclusion that the uncertainty of the total measurement system is too high. But in this case the reason for the high nugget to sill ratio is rather a stable process showing a small variation, thus lowering the sill and therefore inflating the nugget to sill ratio.
The process being monitored, and the attendant on-line quality check of the total measurement system presented by the variogram in Figure 3, is characterised by the fact that the process is dominantly stable, with only a few, isolated deviations. Process stability leads to a well-defined low sill, which in itself is important information for process operators. Low, stable sills carry the main message for such cases: the process does not need controlling. The measurement system also performs well, even if the nugget effect to sill ratio appears to be as high as 45%. In situations where the sill is low, one need not put emphasis on the measurement system quality index, nugget-to-sill ratio, since it is artificially inflated by the low sill.
Iron grade in magnetite slurry
Sampling for iron grade in magnetite slurry is carried out by a completely automated sampling system. The primary sample is also collected here by a shark fin sampler, collecting part of the stream all of the time. The sample is subsequently split and dried before being sent to a robotic X-ray fluorescence laboratory for analysis of Fe, Si, P, V and several other important parameters. Two variograms for this sampling system are presented in Figure 4, representing different time periods of the continuous process operation (these data were previously also published in Reference 5).
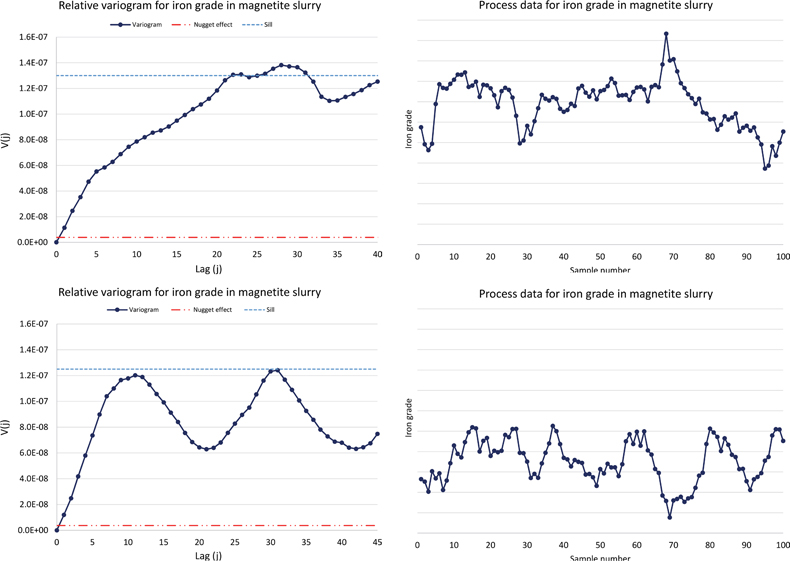
Figure 4. Two variograms for iron grade in magnetite slurry showing different process variability characteristics at different time periods. For a few of the analysed time periods, a clear cyclic behaviour could be identified, see text for detailed interpretation.5
Both variograms show similar nugget effects and similar sill levels. There is, however, one very clear difference as the second variogram shows a clear periodicity of approximately 20 lags or 8–10 hours. Only shorter, isolated time periods exhibit periodicity for this sampling system, but through a continuous variographic characterisation these can be easily detected. Close familiarity with the details of this process makes it likely that periodicity, when detected, is due to fluctuations in the milling capacity, which affects the floatation efficiency and thereby also the iron grade. In some cases, periodicity can also be derived from the sampling system, but this is not considered the case here. Either kind of periodicity is important to recognise and avoid, lest unnecessary and exaggerated process changes might be introduced due to over-corrections. By applying continuously, on-line variographic analysis, it is possible to identify and characterise diverse causes for deviations from stable process conditions. This is possible due to the well-controlled total measurement system characterisations with a nugget to sill ratio of only approximately 5%.
Conclusions
Variographic analysis will in most cases allow meaningful decomposition of observed (raw) process data variabilities into contributions stemming from TSE and/or TAE, revealing the true process variability. The important exception is the case of a low sill, which need not lead to any frustration on behalf of the variogram data analyst, as this case is always signalling that all is well with the process being monitored.
Three typical variogram appearances with different nugget effect to sill ratio characteristics were presented. There are no other cases in practical variographic analysis than either a low sill (in which case all is good due to low process variability) or significantly high(er) sill (also all good, but here with regards to the possibility of variographic decomposition).
Other process data cases and data sets subjected to variographic analysis in the same principal fashion as the present will follow in later instalments of this column, drawn from different application areas in science, technology and industry. There are still interesting aspects of practical variogram interpretation to be learned in this game—stay tuned!
Acknowledgements
The authors wish to express their gratitude to LKAB for allowing this variographic study of current process data and for enable publishing of the results.
References
- R. Minnitt and K.H. Esbensen, “Pierre Gy’s development of the Theory of Sampling: a retrospective summary with a didactic tutorial on quantitative sampling of one-dimensional lots”, TOS Forum Issue 7, 7–19 (2017). https://doi.org/10.1255/tosf.96
- K.H. Esbensen and P. Paasch-Mortensen, “Process Sampling: Theory of Sampling – the Missing Link in Process Analytical Technologies (PAT)”, in Process Analytical Technology, Ed by K. Bakeev. Wiley-Blackwell, pp. 37–80 (2010). https://doi.org/10.1002/9780470689592.ch3
- R. Minnitt and F.F. Pitard, “Application of variography to the control of species in material process streams”, J. S. Afr. Inst. Min. Metall. 108(2), 109–122 (2008).
- F.F. Pitard, Pierre Gy’s Sampling Theory and Sampling Practice, 2nd Edn. CRC Press, Florida (1993).
- K. Engström and K.H. Esbensen, “Evaluation of sampling systems in iron ore concentrating and pelletizing processes - Quantification of Total Sampling Error (TSE) vs. apparent process variation”, Proceedings of MEI Process Mineralogy 16, Cape Town (2016).

