L. Paul Bédarda,* and Kim H. Esbensenb
aLabMaTer, Sciences de la Terre, Université du Québec à Chicoutimi, Chicoutimi, Quebec, Canada. E-mail: [email protected], https://orcid.org/0000-0003-3062-5506
bConsultant at KHE Consulting, Aldersrogade 8, Copenhagen DK-2100, Denmark; guest-, associate-, visiting professor (Denmark, Norway, Puerto Rico, Quebec); E-mail: [email protected]
This practical exercise is aimed at giving students (and other interested parties) a first hands-on experience with the set of primary factors influencing most kinds of “sampling” as occurring in contemporary geoscience, technology and industry. These factors are often ignored or overlooked, but are in fact the most important determinants. Students are asked to count grades (number of occurrences/area) of three clast components in floor terrazzo tiles and to prepare tables, plots and diagrams illustrating their sampling issues. The exercise particularly teaches students to avoid grab sampling, but to use composite sampling instead. For the interested experiment participants, a succinct presentation of relevant introductory literature to the Theory of Sampling (TOS) is also available. This exercise can be viewed as an inspiration, or a role model for possible ways to introduce the TOS to other application sectors as well.
Introduction
Sampling is a critical operation in almost any geoscience undertaking. Its goal is to represent, for example, a rock outcrop, the local soil or in general, the “lot”. A sample that is not representative will lead to erroneous interpretations. In their professional practice, Earth scientists have to sample geological materials (rocks, sediments, soils, mineralisations etc.), but in most cases their training includes only little understanding of the intricate effects on sampling caused by heterogeneous materials. It is fair to say that a dominant part of university geoscience training is restricted to developing a standard sampling approach, one-process-fits-all materials, without serious comprehension of the role played by the widely different degrees of heterogeneity met with in a geoscience career. After field collection, samples are often grain-size reduced and/or mass-reduced (crushed and/or split to smaller masses), steps that are not supposed to modify the original sample, but which will in effect do exactly that if the basic rules of the game (Theory of Sampling, TOS) are not known. Although many parties are often concerned about the quality of the specific analytical protocols used, most of the contributions to the “total measurement uncertainty” (which quantify how the sample taken represents the reality, the lot in the field) actually comes from sampling and sub-sampling instead. There is often a harsh lesson to be learned, both from within the geoscience realm as well as from the TOS. Thus, according to Taylor, Ramsey and Boon1 the uncertainties (errors) associated with sampling can be 10–100 times larger than the uncertainties associated with the chemical analysis per se—which is of course an evergreen observation across the entire TOS field. In this context, understanding sampling must be considered an essential skill for all students in the geosciences. Considering that this is the initial step for most quantitative measurements on which all analytical results and subsequent subject-matter interpretations rely, this short experiment can teach a lot (pun intended).
In the geological context, representativeness is a.o. a function of i) sample size (volume) in relation to grain size, ii) analyte concentration (it is easier to sample for geochemical quantification of major element concentrations for example, than for trace elements) and iii) the spatial distribution of phases.2–5 These factors and their effects on sample representativeness are not necessarily easy to appreciate without some didactic help. Here the Sampling Columns in this publication have met with success,6 and which have recently been developed further into an introductory textbook.7 The present contribution offers a practical exercise to complement these didactic efforts.
Practical testing of the impact of different sampling factors on common, familiar objects, such as floor tiles, allow students to develop an easy, visual hands-on understanding of salient sampling issues and thus prepare them for planning adequate and reliable sampling strategies and protocols for real-world earth science systems, projects and careers. The present exercise specifically addresses the very commonly used grab sampling approach—believing, very often without specific proof, that a single sample will always be representative.
The experiment
Geology students were asked to count identifiable component fragments in multi-phase concrete floor tiles (“terrazzo” tiles), see Figure 1.

Figure 1. Geoscience students hard at work planning tile/sub-tile divisions as a basis for “analysis” (counting and deriving the frequency of component clasts in the terrazzo makeup). The enthusiasm is tangible.
Individual tiles are first divided into several sets of “sub-samples” on which basis students will do simple summary statistics calculations and present the results as graphs (see further below). The students are encouraged to experiment for themselves to learn about the effects of varying sample- and sub-sample size, taking note of the prevailing spatial distribution (heterogeneity) at different scales, and of varying concentration of the analytical elements of interest (fragment type grades in the current example).
A key part of the experiment is to illustrate the influence from the most fundamental sampling determinant, the sampling mode in the form of performing various versions of composite sampling, by adding together an increasing number of individual sub-tile results (correctly termed increments in this context) and to compare these results to the archetype single-increment sampling modus, grab sampling. Finally, they are asked to apply the principles discerned in the experiment to more realistic cases, so they can better comprehend sampling in academic research or industrial contexts. To bring home this lesson with force, reference is made to a particularly powerful and illustrative composite field sampling in the geosciences.8
Measurement
Floor terrazzo tiles (Figures 2 and 3) are used in this experiment because they are made up of many fragments of different type, each characterised by their own typical size, shape, colour and their spatial distribution is significantly heterogeneous (the very allure of terrazzo tiles).

Figure 2. Typical terrazzo tile from the hallways of Sciences de la Terre, Université du Québec à Chicoutimi, with USB stick as scale; see also Figure 3.
Other tile types could easily also have been used as long as clast types are abundant (at least a few hundred within each unit to be counted), of different colour, and of broadly similar shape, so that it is possible to estimate a grade with reasonable realism. If the fragment size varies strongly, the grade estimation (number of clast per area) will be more uncertain, i.e. less realistic. For practical reasons, students are asked to count only fragments larger than 1 cm, partly also to reduce the counting time, see Figure 3.

Figure 3. Overview photograph of a primary floor terrazzo tile as used for the experiments. The field of view measures approximately 30 cm across. Observe the “pleasing” heterogeneous spatial distribution of the three fragment types (pink, black, white); grey fragments were not included in the experiment, see text.
In the building housing Sciences de la Terre, Université du Québec à Chicoutimi, the hallway floor tiles are square and measure approximately 1.8 m (6 feet) along a side. Students are asked to divide these primary tiles in 36 “sub-samples” (6 × 6 sub-tiles, measuring one foot per side). Some students delineated the sub-samples using chalk (which is easy to clean afterward) while others used masking tape. Students were asked to quantify the clast occurrences of all sub-tiles and add them to quantify the whole tile area. For each sub-sample, students count the number of observable rock fragment larger than 1 cm (3⁄8 inch) of each colour: pink, black and white, Figure 3.
“Grey fragments” were to be ignored because they are very small in comparison (less than 1 cm), i.e. too numerous and counting time becomes unreasonable for a 3 h laboratory period. If a fragment is crossed by one of the dividing lines (or tape), the “centre of gravity” rule applies: if the fragment centre of gravity falls inside the sub-tile delineation, the fragment is included.2–4
In addition to this 2-D sampling exercise, the students would also be asked to delimit a thin perpendicular band of ~2 cm width (1 inch would also do) 30 cm (1 foot) and 60 cm (2 feet) away from one side, to simulate an alternative drill core sub-division.
The students were asked to compile their data in tables (Table 1). These measurements all-in-all take about one hour for a team of two undergraduate students. There were five student teams participating in the experiment. Individual teams “sampled” different primary tiles in an attempt to simulate true heterogeneous field relationships.
Table 1. Example of basic fragment counting for all 36 sub-samples from one primary terrazzo tile.
Sub-sample | 1 | 2 | 3 | 4 | 5 | 6 |
A | B = 10 P = 24 W = 7 | B = 9 P = 17 W = 7 | B = 5 P = 25 W = 10 | B = 7 P = 25 W = 7 | B = 2 P = 37 W = 8 | B = 7 P = 37 W = 11 |
B | B = 6 P = 29 W = 6 | B = 9 P = 16 W = 4 | B = 5 P = 25 W = 5 | B = 5 P = 26 W = 2 | B = 9 P = 28 W = 5 | B = 15 P = 31 W = 8 |
C | B = 5 P = 22 W = 11 | B = 5 P = 24 W = 8 | B = 7 P = 26 W = 13 | B = 7 P = 19 W = 6 | B = 13 P = 34 W = 5 | B = 3 P = 21 W = 7 |
D | B = 6 P = 20 W = 4 | B = 9 P = 26 W = 6 | B = 5 P = 19 W = 5 | B = 7 P = 16 W = 9 | B = 9 P = 40 W = 9 | B = 7 P = 37 W = 11 |
E | B = 9 P = 19 W = 7 | B = 5 P = 18 W = 5 | B = 3 P = 27 W = 5 | B = 6 P = 15 W = 5 | B=4 P = 30 W = 5 | B = 3 P = 18 W = 7 |
F | B = 7 P = 21 W = 5 | B = 6 P = 41 W = 5 | B = 3 P = 31 W = 6 | B = 3 P = 18 W = 3 | B = 8 P = 21 W = 9 | B = 6 P = 21 W = 7 |
B: black fragments, P: pink fragments, W: white fragments
Calculations
Students have to compute the grade (number of fragment/area) for each sub-sample, and the relative standard deviation of all 36 sub-samples for the three analytes (or “elements”): types (colours) of fragment. The sub-sample results were then used to create aggregate composite samples made up from 2, 3, 4, 6, 9, 12, 18 and 36 increments (sub-samples). Finally, they were requested to draw a diagram of grade determination variability, i.e. count relative standard deviations against the number of increments (sub-samples) in the composite sample (Figure 4).
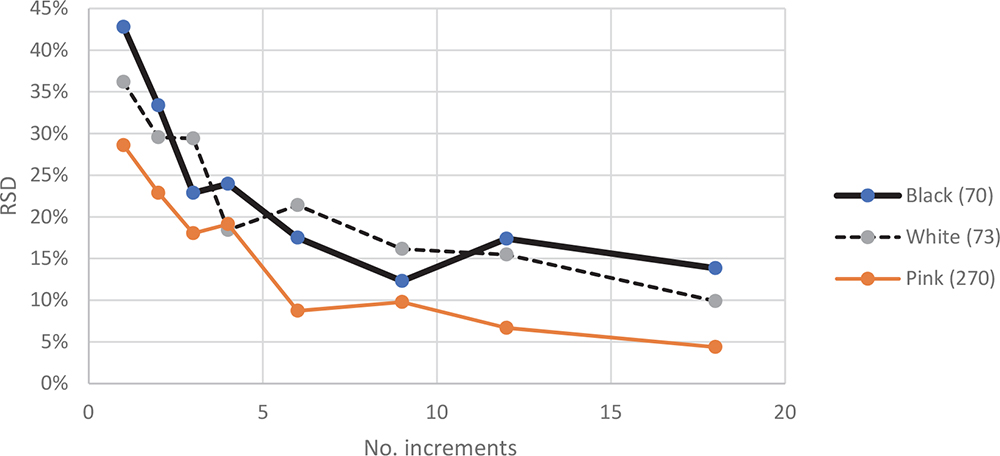
Figure 4. Graph showing the relative standard deviation of composite sampling results as the number of increments increases. The number in parenthesis is the number of fragments per m2 corresponding to a full tile.
Interpretation
A set of didactic questions were asked to guide the exercise, such as:
- How reproducible are the 36 single grab sampling results relative to the true grade (i.e. that of the whole tile) for the three analyte colours?
- Is there a discernible relationship between grade and sampling error?
- How many increments are necessary in a composite sample to obtain a “reasonable” stable sampling error?
- How reproducible are the “drill core” sub-sample results relative to the true grade of the whole tile for the same three “analytes”?
The students were finally also asked to assess and describe the quantitative importance of the influential factors studied relative to observed and calculated sampling errors. This is aimed at allowing the students to acquire a first hands-on experience and knowledge with which better to undertake similar sampling issues in later real-world situations.
After joint discussions of the results from the different student groups, focusing on the differences encountered at different scales, it was the intention that students should now be better equipped, and better motivated—and have developed an interest in getting a professional attitude and competence—regarding sampling. They are at this time, needless to say, also presented with a compact TOS literature documentation.
Discussion
Tables 1–3 and Figure 4 illustrate examples of the results of one team effort on a single tile. In Table 2, the grade for each sub-sample for black fragments varies from 21 to 161 fragment/m2, compared to the whole tile whose grade is 70 fragment/m2 and Table 3 shows that results for composite samples of four sub-samples show grade (fragment/m2) variations from 40 to 91 while the whole tile grade is the same 70 fragment/m2. Students can easily appreciate that composite sampling results in much smaller variations and that these estimated grades (“analyte concentrations”) are much closer to the “truth” (the whole tile grade). From Table 3 and Figure 4, they can appreciate that the sampling error (relative standard deviation in %) for each composite sample is reduced as the number of aggregate increment increases.
Table 2. Example of results (grade; black fragment/m2) for each sub-sample; total tile grade = 70 fragment/m2.
Sub-sample | 1 | 2 | 3 | 4 | 5 | 6 |
A | 107 | 97 | 54 | 75 | 21 | 75 |
B | 64 | 97 | 54 | 54 | 97 | 161 |
C | 54 | 54 | 75 | 75 | 140 | 32 |
D | 64 | 97 | 54 | 75 | 97 | 75 |
E | 97 | 54 | 32 | 64 | 43 | 32 |
F | 75 | 64 | 32 | 32 | 86 | 64 |
Table 3. Example of results (grade; black fragment/m2) for composite sample of four sub-samples; total tile grade = 70 fragment/m2.
| 1’ | 2’ | 3’ |
A’ | 91 | 59 | 89 |
B’ | 67 | 70 | 86 |
C’ | 73 | 40 | 56 |
Students noted a.o. that sampling variability depends on general “analyte concentration” levels (lowest for the “pink” fragment phase which has the highest concentration level), as well as “interchanging” sampling variabilities between the broadly similar “white” and “black” fragment—a reflection of the Fundamental Sampling Error (FSE) corresponding to the particular type of heterogeneity displayed by this “rock type”. When addressing the thin “drill core” simulation, they can also well appreciate the relative sampling variability magnitudes of such comparatively smaller sample sizes (areas), which are significantly larger. A fruitful discussion of the validity of drill core samples can often be established, often making the participants think very carefully about using the same drill core diameter for many types of rocks, rocks of potentially very different nature—all very useful stuff for students of geology.
Table 4. Example of grade and relative standard deviation calculation for each fragment (colour).
| Black | White | Pink |
Whole tile grade (fragment/m2) | 70 | 73 | 270 |
RSD: Increment = 1 (%) | 43 | 30 | 23 |
RSD: Increment = 2 (%) | 33 | 29 | 23 |
RSD: Increment = 3 (%) | 20 | 29 | 18 |
RSD: Increment = 4 (%) | 24 | 18 | 19 |
RSD: Increment = 6 (%) | 17 | 21 | 9 |
RSD: Increment = 9 (%) | 12 | 16 | 5 |
RSD: Increment = 12 (%) | 17 | 15 | 7 |
RSD: Increment = 18 (%) | 14 | 10 | 4 |
Conclusions
A simple, short practical exercise is aimed at giving students hands-on experience with a set of the most important primary factors influencing “sampling” as occurring in contemporary science, technology and industry, specifically factors grab vs composite sampling, which are very often ignored or overlooked, but which are in fact the most important determinants. There is a world of difference between not knowing about, and therefore performing grab sampling, and understanding the advantages of the composite sampling alternative. This entry level exercise is specifically meant to raise student interest in the ensuing, more challenging aspects of sampling, which are not necessarily “intuitive”. Experience in Quebec with this exercise is highly satisfactory.
Acknowledgements
The students of the 2017 geostatistic class (A. Brochu, A. Chassagnol-Dumur, G. Cyr, D. Morel, F. Noel-Charrest, C. Ouellet, M. Paradis, L.-P. Perron-Desmeules and R. Tremblay) are thanked for sharing their data and experience. May the sampling force be with them in their future careers.
Epilogue
The basic didactic setup used in this exercise has also been the guideline for other endeavours, some concerning more advanced professional studies of rock heterogeneity. As one of several examples, the mineralogic heterogeneity of a South African white, two-feldspar granite, which is popular and much used as floor tiles in several international airports, has been characterised by the use of image analysis, automatically recognising five mineralogic phases and their grades (there is a lot of image analysis going on here!).
Several groups of students have been photographing scores of tiles with an accumulated area of ~hundred square metres, allowing a rare big volumetric characterisation of granite heterogeneity (or its reciprocal, uniformity), never possible before. Results for several hundred tiles across these five “variables” (mineralogical phase grades) necessitate a multivariate data analysis approach, chemometrics, see, for example, Reference 9; such results are planned to be presented elsewhere.
An indication of the ambition level of such studies is shown by Figure 5 (left).

Figure 5. Two very different airport tile types (researcher POV), the one to the right is the South African white, two-feldspar granite mentioned in the Epilogue. Note the considerably more complex, partially deformed red granite type to the left, which can also be subjected to image analytical characterisation, although this constitute a much more ambitious image acquisition and data analysis task.
References
- P.D. Taylor, M.H. Ramsey and K.A. Boon, “Estimating and optimising measurement uncertainty in environmental monitoring: An example using six contrasting contaminated land investigations”, Geostand. Geoanal. Res. 31(3), 237–249 (2007). https://doi.org/10.1111/j.1751-908X.2007.00854.x
- F.F. Pitard, The Theory of Sampling and Sampling Practice, 3rd Edn. CRC Press (2019). ISBN: 978-1-138476486
- P. Gy, Sampling for Analytical Purposes. Elsevier, Netherlands (1998).
- L. Petersen, P. Minkkinen and K.H. Esbensen, “Representative sampling for reliable data analysis: Theory of Sampling”, Chemometr. Intel. Lab. Syst. 77(1–2), 261–277 (2005). https://doi.org/10.1016/j.chemolab.2004.09.013
- DS 3077. Representative sampling—Horizontal Standard, 2nd Edn. Danish Standards (2013). http://www.ds.dk
- K.H. Esbensen and C. Wagner, Sampling Columns in Spectroscopy Europe. https://www.spectroscopyeurope.com/sampling
- K.H. Esbensen, Introduction to Theory and Practice of Sampling. IM Publications Open, UK (2020). ISBN: 978-1-906715-29-8, https://www.impopen.com/sampling
- K.H. Esbensen and P. Appel, “Barefoot sampling in San Juan de Limay, Nicaragua: remediation of mercury pollution from small scale gold mining tailings”, TOS Forum Issue 7, 3–9 (2017). https://doi.org/10.1255/tosf.98
- K.H. Esbensen and B. Swarbrick, Multivariate Date Analysis—An introduction to Multivariate Data Analysis, Process Analytical Technology and Quality by Design. CAMO (2018). ISBN: 978-82-69110-40-1


