Pentti Minkkinen
Professor emeritus, Lappeenranta Lahti University of technology (LUT), Finland and President, Senior Consultant, Sirpeka Oy, Finland
DOI: https://doi.org/10.1255/sew.2021.a25
© 2021 The Author
Published under a Creative Commons BY licence
Sampling for analysis is a multi-stage operation, from extracting a primary sample (s1) via sub-sampling (s2) … (s3) towards the final analytical aliquot (s4). At each stage, a sampling error is incurred if not properly reduced or eliminated, collectively adding to the error budget. Nobody wants the total measurement error to be larger than absolutely necessary, lest important decisions based thereupon are seriously compromised. However, it is in the interregnum between sampling and analysis where one finds plenty of usually unknown hidden costs, lost opportunities and a bonanza of bold, red figures below the bottom line. We have asked one of the peers of sampling, with extensive industrial and technological experience, to focus on the economic consequences of not engaging in proper sampling. Enjoy these “horror stories” from which we can all learn, not least at management level.
Along the full lot-to-analysis pathway
Analytical measurements comprise at least two error generating steps: delineating and extracting the primary sample, and analysis of the analytical aliquot. There may be several sub-sampling steps before having a sufficiently small aliquot (analytical sample) of the original material ready for proper analysis. In this chain of operations, the weakest link determines how reliable the analytical result is. The reason is that variances (squared standard deviations) are additive.
If only one primary sample is processed through i stages, the error variance of the analytical result, aL is:
$$s_{{a_L}}^2 = \mathop \sum \limits_{i = 1}^I s_i^2$$
(1)
This variance can be reduced (always popular for those who worry about the total sampling-plus-analysis error) by taking replicate samples at different stages. Consider a three-level process: n1 primary samples are extracted from the lot, with each primary sample processed and divided into n2 secondary samples—of which nlab analytical samples are finally analysed. In this case Equation 2 shows how the complement of stage error variance components propagate to the analytical result.
$$s_{{a_{\rm{L}}}}^2 = {{s_1^2} \over {{n_1}}} + {{s_2^2} \over {{n_1} \bullet {n_2}}} + {{s_{{\rm{lab}}}^2} \over {{n_1} \bullet {n_2} \bullet {n_{{\rm{lab}}}}}}$$
(2)
The total number of samples analysed is ntot = n1 • n2 • nlab.
From a replication design, the variance components si2 can be estimated by using the statistical facility of analysis of variance (ANOVA), or analysis of relative variances (RELANOVA).1
Master example: the effectiveness of replication
The following example will help gain insight into where efforts to reduce and control the total accumulated error is best spent. Let us consider three schemes where, for each scheme, the relative standard deviation error estimates are: sr1 = 10 %, sr2 = 4 % and sr2 = 2 %.
No replicates, n1 = n2 = nlab = 1. Total number of samples analysed is 1.
$$s_{{a_{\rm{L}}}}^2 = {\left( {10\,\% } \right)^2} + {\left( {4\,\% } \right)^2} + {\left( {2\,\% } \right)^2} = 120\;{\left( \% \right)^2}\;{\rm{and}}\;{s_{{a_L}}} = 11.0\;\,\% $$
Primary samples replicated, n1 = 10; n2 = nlab = 1. Total number of samples analysed is 10.
$$s_{{a_L}}^2 = {{{{\left( {10\,\% } \right)}^2}} \over {10}} + {{{{\left( {4\,\% } \right)}^2}} \over {10}} + {{{{\left( {2\,\% } \right)}^2}} \over {10}} = 12.0\;{\left( \% \right)^2}\;{\rm{and}}\;{s_{{a_L}}} = 3.5\,\% $$
Primary samples and duplicated analytical samples, n1 = 5; n2 = 1; nlab = 2. Total number of samples analysed is again 10.
$$s_{{a_L}}^2 = {{{{\left( {10\,\% } \right)}^2}} \over 5} + {{{{\left( {4\,\% } \right)}^2}} \over {5 \bullet 1}} + {{{{\left( {2\,\% } \right)}^2}} \over {5 \bullet 1 \bullet 2}} = 23.6\;{\left( \% \right)^2}\;{\rm{and}}\;{s_{{a_L}}} = 4.9\,\% $$
This example demonstrates that even if the best and most expensive analytical technology available is used in the laboratory, this does not by itself guarantee a reliable result with minimised total uncertainty. Still, some laboratories routinely run analyses in duplicates or even in triplicates to be sure that their results are “correct”. While analytical costs have doubled or tripled, nothing is gained! It is also common that the uncertainty estimates which laboratories assign to their results are based on the results of the laboratory replicates only; in reality hiding the full pathway uncertainty.
Selection of optimal sampling mode
Most current standards and guidelines assume glibly—although very rarely expressed explicitly—that sampling errors can be estimated using standard statistics. This is based on another assumption, that of a random spatial analyte distribution within the sampling target. When primary samples are extracted from large lots like process streams, environmental targets, shipment of raw materials or commodities or from manufactured products, the same assumption of “normality” may in fact lead to sampling plans that are more expensive than the optimised plan and, more importantly, do not provide reliable results. When the purpose of sampling is to estimate the mean value of the lot, the first issue to address is which sampling mode to use: random, stratified or systematic. Figure 1 shows and compares the principle of these modes. Very few guidelines refer to the sampling modes at all. Very often in monitoring programmes samples are collected systematically (all good), but the resulting analytical results are then treated as so-called random data sets. As the following example shows this actually results in a massive loss of information.
Figure 1 presents a comparison of these three fundamental sampling modes as applied to a process steam. First, there is no significant difference between them if the process standard deviation is estimated from all nine samples taken in each mode, i.e. the nine samples are treated as one data set. But their difference becomes clear when the mean of the whole process range is calculated. The bias of the mean is decreased from 4.49 % (random) to 3.92 % (stratified) and to –0.48 % (systematic) and the relative standard deviation of the mean from 11.3 % (random) to 8.28 % and to 2.26 %. The difference is even more clear if, based on these data, a sampling plan is requested, for example, with a target that the relative standard deviation of the mean shall not exceed 1 %. The “expert” who recommends random sampling gives a plan that requires extraction of no less than 385 samples. However, a stratified sampling plan will only require 186 samples—whereas if the systematic mode is selected, only 12 samples are needed to reach the relative standard deviation target. To summarise, in cost–benefit analysis of an analytical sampling plan the selection mode is crucial.
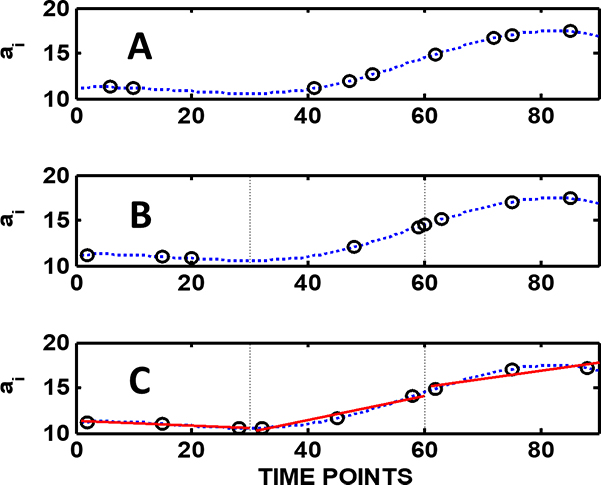
Figure 1. A: Random sampling: sampling times or locations are selected randomly. B: In stratified (random) sampling the process lot is divided into individual strata (three strata in this example) and within each stratum the sampling points are selected randomly. C: In systematic sampling the within-stratum samples are all taken at fixed intervals. The continuous line is based on process analyser measurements at short time intervals. For all three cases the lot average aL = 13.193, the relative sampling and analysis variance sr2 = 6.962 and relative standard deviation sr = 0.20 (= 20 %).
To select the optimal sampling mode and number of replicates, the unit costs are needed. Operators usually can estimate the cost structure, but the variance estimates can seldom be estimated theoretically. Sometimes they can be estimated from the existing data, but very often pilot studies are needed. Combining specific variance estimates with unit costs of the various operations in the full analytical measurement pathway will allow drastic improvements in the efforts needed; some examples are given below. Further examples of the informed use of the Theory of Sampling (TOS)’ principles in the context of total expenditure estimation are given in Reference 2.
The value of engaging in proper sampling
Case 1
A pulp mill was extracting a valuable side product (β-sitosterol) which is used in the cosmetic and medical industries, and which has high quality requirement. Customers requested a report on the quality control system from the company in question. I was asked to audit the sampling and analytical procedures and to give recommendations, if needed. I proposed some pilot studies to be carried out and based on these empirical results recommended a new sampling system to be implemented—this was accepted.
In comparison to the old, the new sampling system annually saved the equivalent of one laboratory technician’s salary.
Case 2
An undisclosed pulp mill was feeding a paper mill through a pipeline pumping the pulp at about 2 % “consistency” (industry term for “solids content”). The total mass of the delivered pulp was estimated based on the measurements with a process analyser installed in the pipeline immediately after the slurry pump at the pulp factory. The receiving paper mill claimed that it could not produce the expected tonnage of paper from the tonnage of pulp they had been charged for by the pulp factory. An expert panel was asked to check and evaluate the measurement system involved. A careful audit, complemented with TOS-compatible experiments, revealed that the consistency measurements were biased, in fact giving up to 10 % too high results. The bias was found to originate from two main sources. 1) The process analyser was placed in the wrong location and suffered from a serious increment delimitation error; this is an often-met weakness of process analysers installed on or in pipelines. 2) The other error source was traced to the process analyser calibration. It turned out that the calibration was dependent on the quality of the pulp: softwood and hardwood pulps needed different calibrations. By a determined effort to make the process sampling system fully TOS-compatible, and by updating the analyser calibration models, it was possible to fully eliminate the 10 % bias detected.
It is interesting to consider the payback time for the efforts involved to focus on proper TOS in this case. The pulp production rate was about 100,000 ton y–1, or 12 ton h–1. The contemporary price of pulp could be set as an average of $700 ton–1, so the value produced per hour was approximately $8400 h–1. The value of the 10 % bias would thus be $840 h–1 ($7 million y–1). As the cost of the evaluation study was about $10,000 the payback time of the audit and the panel investigations was about 12 h.
It does not have to be expensive to invoke proper TOS competency—it is often possible to get a better quality at lower cost.
Are our current sampling standards and guides adequate?
In most current standards, the findings of the TOS have often been ignored, or at best only partially recommended. Statistical considerations assume that sampling errors can be estimated using classical statistics which are based on the ubiquitous assumption of random spatial analyte distributions within the sampling targets. The basic three sampling modes, random, stratified or systematic, are seldom even mentioned as options. As shown above, when primary samples are taken from large lots like process streams, environmental targets, shipment of raw materials or products, ill-informed or wrong assumptions simply lead to wrong conclusions, and usually too expensive or inefficient solutions. More examples are given below.
Case 3: Estimation of the concentration genetically modified (GMO) soybeans
In the European Union, the limit of acceptable GMO content in soybeans is 1 % (or 1 GMO bean/100 beans). If the content exceeds this limit, the lot must be labelled as containing GMO material. To allow for the sampling and analytical error, in practice 0.09 % is used as the effective threshold limit for deciding on labelling the material as containing GMO or not. Theoretically, this seems a simple sampling and analysis problem. GMO soybeans and their natural counterparts are identical with no tendency to segregate. So, theoretically the required sample size can be estimated from considerations assuming a binomial distribution. The reality is very different, however.
In References 3–5 experimental analytical data from the KeLDA project were re-analysed, with a special focus on the inherent sampling issues involved. In the KeLDA project, 100 shiploads arriving at different EU ports were sampled by collecting 100 primary 0.5-kg samples (each containing approximately 3000 beans) using systematic sampling. At the 1 % concentration level, the relative standard deviation of the total analytical error (sTAE) was found to be 11.4 %. For an ideal binomial mixture, conventional statistical calculations showed that the minimum number of 0.5-kg samples to be analysed in order to guarantee that the probability (risk) is less than 5 % that the mean 0.09 % could be from a lot having mean concentration above 1 %—is 10 samples. The official number of samples recommended by many organisations vary between 4 and 12. So far, so good... if the conventional assumptions hold up to reality… alas!
A shipload often consists of products from many different sources having different GMO concentrations. In such cases the lot can be seriously segregated in the distributional sense w.r.t. domains having different GMO contents, making the assumption of spatial randomness grossly erroneous. Instead of the theoretical 10 samples, the thorough study reported in Reference 4 (lots of statistics in there, but they are not necessary for the present purpose) ended up with a much higher required number of samples needed, 42 to be precise (a famous number, if the reader is fan of Douglas Adams’ Hitchhiker’s Guide to the Galaxy). It is this number of samples which must be collected using the systematic sampling mode to make a correct decision regarding the labelling issue.
From enclosed stationary lots, such as the cargo hold(s) of grain shipments, or truckloads, railroad cars, silos, storage containers… it is in general impossible to collect representative samples without a TOS intervention. Samples must be taken either during loading or during unloading of the cargo, i.e. when the cargo lot is in a moving lot configuration on a conveyor belt. Otherwise, the average concentration simply cannot be reliably estimated. References 3–5 tell the full story, the conclusion of which is: conventional statistics based on the assumption of spatial random analyte distributions always runs a significant risk of underestimating the number of samples needed to reach a specified quality specification—compared to informed TOS-competent understanding of heterogeneity, spatial heterogeneity in this case. Proper TOS-competence is a must.
Case 4: Sampling for aflatoxins in peanut kernels
Mycotoxins, e.g. aflatoxins and ochratoxins, are poisonous and are also regarded as potent carcinogens. Their contents in foodstuff must, therefore, be carefully monitored and controlled and the levels regarded safety are extremely low, down to 5 µg kg–1 (ppm), or even lower. But detection and quantification even of these very low concentration levels is usually not a challenge for modern analytical techniques in dedicated analytical laboratories. The real challenge is how to provide a guaranteed representative analytical aliquot (of the order of grams only) from the type of large commercial lots used in the international trade of such commodities (of the order of magnitude of thousands of tons). Effective sampling ratios are staggering, e.g. 1 : 106 to 1 : 109, or even higher. It is somebody’s responsibility that the overwhelming 1 / 106 to 1 / 109 mass reduction is scrupulously representative at/over all sampling and sub-sampling stages. It is fair to say, that this setup is not always known, recognised, far less honoured in a proper way, sadly (because this is where the money is lost, big time) with the unavoidable result that nobody (nor any guideline or standard) can guarantee representativity.
Campbell et al.6 carried out an extensive sampling study in connection with analysing peanuts for aflatoxins. It is interesting to study their findings using the principles of TOS: they sampled a lot having an average aflatoxin content 0.02 mg kg–1 by taking 21.8 kg primary samples. The average aflatoxin content of individual “mouldy” peanut kernels was 112 mg kg–1. The average mass of one peanut kernel is about 0.6 g. In Reference 6 it was found that the experimental relative standard deviation of the 21.8-kg primary samples sr(exp) was 0.55 = 55 %. This empirical result exceeds the theoretically expected value, however, indicating that “something” is not right … A TOS rationale follows below.
Involving TOS
The mass of aflatoxin in a single mould contaminated kernel: ma = 112 mg kg–1 × 0.6 × 10–3 kg = 0.0672 mg. If the acceptable average aflatoxin level is 0.02 mg kg–1, this result means that just one mouldy peanut is enough to contaminate a whole sample of 3.36 kg. On the other hand, if the maximum tolerable level is only 0.005 mg kg–1, one kernel will contaminate a 13.44-kg sample. If the kernels are crushed to 50 mg fragments, average samples containing one contaminated fragment are now 0.28 kg and 1.12 kg at average aflatoxin concentrations 0.02 mg kg–1 and 0.005 mg kg–1, respectively. The relative standard deviation of a sample containing one contaminated peanut taken from a random distribution is 1 = 100 %.
The theoretical relative standard deviation of a 21.8-kg sample from a random mixture is sr = 39.3 % whereas the experimental value was 55 %. The difference between these variance estimates [0.552 – 0.3932 = 0.148, or 38.5 % as RSD %] is a strong indication of spatial segregation. Such segregation of mycotoxins in large lots is a natural phenomenon, since moulds, which are producing the toxins, tend to grow in localised “pockets” where mould growth conditions are favourable. As an unavoidable consequence, the distribution of contaminated individual nuts within the full lot volume is in reality far from random. Because large lots, almost exclusively found in restricted and confined containers, cannot be well mixed (randomised), segregation has a drastic adverse effect on sampling uncertainty at the primary sampling stage—whereas at all later sample preparation stages, when only small masses are handled, it is possible to randomise various sized sub-samples by careful mixing, and here the theoretical values can be used to estimate the uncertainty of the sub-sampling steps involved.
For the ideal case of truly random mixtures, it is easy to estimate the sample size that gives the required relative standard deviation of the lot as a function of the primary sample size. For the two lot averages used here as examples, aL is 0.02 mg kg–1 and 0.005 mg kg–1, and targeting to 10 % relative standard deviation of the lot mean, the realistic minimum sample sizes are:
$${m_s} = {{{{\left( {100\,\% } \right)}^2}} \over {{{(10\,\% )}^2}}}3.36\;\,{\rm{kg}} = \;\;{\bf{336\;}}\,{\bf{kg}}$$
$${m_s} = {{{{\left( {100\,\% } \right)}^2}} \over {{{(10\,\% )}^2}}}13.44\,\;{\rm{kg}} = \;\;{\bf{1344}}\,{\bf{\;kg}}$$
If the distribution is indeed random, the ms can be a composite sample or single increment, the expected RSD of the mean is the same, 10 %, independent of the sampling mode. But the situation is radically different if there is indeed segregation, e.g. clustering of the contaminated peanuts. Then the required primary sample size and number will depend on the spatial distribution pattern and this can only be estimated empirically, either by a variographic experiment or by involving an ANOVA design, see References 3–6.
The only result that can be estimated from the reported data in the Campbell et al. study, is how many 21.8-kg samples, nreq, are needed if random sampling is used. If the target threshold is 10 % RSD of the mean at aL = 0.02 mg kg–1:
$${n_{s\left( {{\rm{req}}} \right)}} = \;{{s_{r\left( {{\rm{exp}}} \right)}^2} \over {{{\left( {10\,\% } \right)}^2}}} = {{{{(55\,\% )}^2}} \over {{{\left( {10\,\% } \right)}^2}}} = 30.3$$
and the total mass of the samples 30.3 • 21.8 kg ≈ 660 kg.
Implications for commodity trade a.o.
In international trade agreements regarding foodstuffs, the tight limits set by regulators must be met at the entry port before the cargo materials can be released to the markets. As the examples above show, sampling and sample preparation for analysis are extremely difficult when the unwanted contaminants are present at their usual low, or very low ppm (or even ppb) levels. In the case of the present peanut example, at an average concentration 5 µg kg–1 in an ideal case (i.e., assuming randomness), the weight of the total number of primary samples should be about 1350 kg if the if 10 % relative standard deviation is the target. In sample preparation, if the secondary samples are each 10 kg and the analytical sample from which the toxins are extracted, are, say, 200 g, the peanuts must be ground to 0.45 mg and 0.09 mg particle sizes corresponding to approximately 0.96 mm and 0.56 mm particle diameters. But these are the results of an ideal case, very rarely found. Segregation makes the theoretical considerations much more complicated.
The simple moral from underlying complexities
The above technical intricacies notwithstanding, it is abundantly clear, that the quality of sensitive foodstuffs must be adequately monitored—and it is equally clear that at the inherent trace and ultra-trace levels of the analytes involved, the primary sampling and sample preparation are extremely difficult operations, but absolutely necessary! If the uncertainties of the analytical results are too high, this means that a high number of shipments containing excess amount of the contaminants may enter the market essentially undetected and, vice versa, shipments containing acceptable material may be stopped—but both types of misclassification are not caused by analytical difficulties. The resulting economic losses are huge, for each shipload that is wrongly stopped and retuned due to “erroneous” analytical results. The lesson from the somewhat technical story above is clear: primary sampling, and subsequent sub-sampling and sample preparation errors, are very nearly always the real culprits—perpetrators are not to be found in analytical laboratories.
What to do?
When decision limits are set, the capability of modern analytical instruments alone cannot be used as the guide for reliability. The capability of the whole measurement chain must be evaluated. If it turns out that the proposed decision limit is so low that it cannot be achieved at acceptable costs, even when the best methods of the TOS are applied in designing the sampling and measurement plan, then it must be decided what are the maximum allowable costs of the control measurements. First, then is it possible to set realistic decision limits so that they can be reached with methods optimised to minimise the uncertainty of the full lot-to-aliquot measurement pathway within a given budget which is regarded as acceptable; a more fully developed treatment of these interlinked technical and economic factors can be found in References 1 and 2.
References
- P. Minkkinen, “Cost-effective estimation and monitoring of the uncertainty of chemical measurements”, Proceedings of the Ninth World Conference on Sampling and Blending, Beijing, China, pp. 672–685 (2019).
- P. Minkkinen, “Practical applications of sampling theory”, Chemometr. Intell. Lab. Syst. 74, 85–94 (2004). https://doi.org/10.1016/j.chemolab.2004.03.013
- K.H. Esbensen, C. Paoletti and P. Minkkinen, “Representative sampling of large kernel lots I. Application to soybean sampling for GMO control”, Trends Anal. Chem. 32, 154–164 (2012). https://doi.org/10.1016/j.trac.2011.09.008
- P. Minkkinen, K.H. Esbensen and C. Paoletti, “Representative sampling of large kernel lots II. Theory of sampling and variographic analysis”, Trends Anal. Chem. 32, 165–177 (2012). https://doi.org/10.1016/j.trac.2011.12.001
- K.H. Esbensen, C. Paoletti and P. Minkkinen, “Representative sampling of large kernel lots III. General considerations on sampling heterogeneous foods”, Trends Anal. Chem. 32, 178–184 (2012). https://doi.org/10.1016/j.trac.2011.12.002
- A.D. Campbell, T.B. Whitaker, A.E. Pohland, J.W. Dickens and D.L. Park, “Sampling, sample preparation, and sampling plans for foodstuffs for mycotoxin analysis”, Pure Appl. Chem. 58(2), 305–314 (1986). https://doi.org/10.1351/pac198658020305

Pentti Minkkinen
Pentti Minkkinen received his MSc (eng.) from Helsinki University of Technology in 1969. He then worked as an Associate Expert in two UN Development Program mineral exploration projects in Turkey and in Egypt before completing his graduate studies at Helsinki. In 1976, he started as Associate Professor (Inorganic and Analytical Chemistry) at a newly founded University, Lappeenranta University of Technology, from which retired as full professor by the end of 2007, after a 40+ year tenure. Here he started teaching the theory and applications of sampling in 1978, soon also chemometrics, as an important part of process analytical chemistry. He has been lecturing sampling at undergraduate and graduate courses at several universities, at professional continuing education courses, and at numerous conferences and at industry courses. After retirement, he worked three periods as Visiting Professor at Aalborg University, Campus Esbjerg, Denmark in Prof. Esbensen’s research group (2007, 2008 and 2009). In 2012, he founded Sirpeka Oy from which he offers consulting services on sampling, analytical quality control and in chemometrics. At his old university, now amalgamated and named Lappeenranta Lahti University of Technology (LUT), he continues his scientific career as Professor emeritus. Prof. Minkkinen was the founding chairman of the continuing biannual conference series, Scandinavian Symposium of Chemometrics. He was also co-chairman for the first World Conference on Sampling and Blending. He is the founding chairman of the Discussion Group of Chemometrics in the Finnish Chemical Society. He has published ~80 papers on chemometrics and sampling in refereed journals and conference proceedings; his invited and contributed lectures in various conferences and symposia contributions is close to 200. He has received three international awards: The Kowalski Prize in Chemometrics (2002), the Herman Wold Gold Medal in Chemometrics (2007) and the Pierre Gy Sampling Gold Medal (2007); he is the only recipient of all three distinguished awards. 0000-0002-0918-0234
0000-0002-0918-0234
[email protected]; [email protected]

